|
|
【纪念当年的帖子(2010)】Add Maths功课讨论区
 [复制链接]
[复制链接]
|
|
|
 发表于 8-3-2010 09:01 PM
|
显示全部楼层
发表于 8-3-2010 09:01 PM
|
显示全部楼层
|
我现在很烦恼,SPM要到了,每科功课都还没准备好。这几天正在赶add maths。我现在遇到麻烦,form 4第二课有几题不会。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 09:03 PM
|
显示全部楼层
发表于 8-3-2010 09:03 PM
|
显示全部楼层
Given that -3 and k are the roots of the quadratic equation.(2x+1)(x-1)=p(1-3x), where p is a constant, find the value of p and of k.
不会不会,救命。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 09:04 PM
|
显示全部楼层
发表于 8-3-2010 09:04 PM
|
显示全部楼层
Given that -3 and k are the roots of the quadratic equation.(2x+1)(x-1)=p(1-3x), where p is a constant, find the value of p and of k.
不会不会,救命。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 09:08 PM
|
显示全部楼层
发表于 8-3-2010 09:08 PM
|
显示全部楼层
本帖最后由 Enceladus 于 8-3-2010 09:09 PM 编辑
The roots of the quadratic equation x^2+3x=10 are p+1 and q-1. Find the values of p and the corresponding values of q.这题也是不会。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 09:26 PM
|
显示全部楼层
发表于 8-3-2010 09:26 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 10:26 PM
|
显示全部楼层
发表于 8-3-2010 10:26 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2010 10:29 PM
|
显示全部楼层
发表于 8-3-2010 10:29 PM
|
显示全部楼层
|
walao,原来是同样做法,我懂了,谢谢你的教导。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-3-2010 10:59 PM
|
显示全部楼层
发表于 9-3-2010 10:59 PM
|
显示全部楼层
xy=(-2/3)(x+y)+6
xy:Y,(-2/3)=m,x+y=X,6=C
Find the y in terms of x.
最不不会就是in terms of这些了 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-3-2010 02:13 PM
|
显示全部楼层
x(x-7)<18
find value of x .
看看这题 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-3-2010 03:47 PM
|
显示全部楼层
发表于 10-3-2010 03:47 PM
|
显示全部楼层
回复 189# superliong
x^2-7x<18
x^2-7x-18<0
(x-9)(x+2)<0
-2<x<9 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-3-2010 03:52 PM
|
显示全部楼层
发表于 10-3-2010 03:52 PM
|
显示全部楼层
本帖最后由 walrein_lim88 于 10-3-2010 03:54 PM 编辑
xy=(-2/3)(x+y)+6
xy:Y,(-2/3)=m,x+y=X,6=C
Find the y in terms of x.
最不不会就是in terms of这些了: ...
永遠愛著許瑋倫 发表于 9-3-2010 10:59 PM 
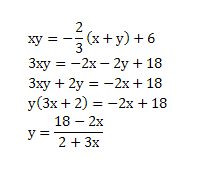 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-3-2010 04:43 PM
|
显示全部楼层
Given f(x)=6-3k+6kx-3x^2
where k is constant.
Show that the equation of the axis of symmetry of the graph of f(x) is x = k.
Then , find the value of k if f(x)has a maximum value of 12 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-3-2010 05:34 PM
|
显示全部楼层
发表于 10-3-2010 05:34 PM
|
显示全部楼层
Given f(x)=6-3k+6kx-3x^2
where k is constant.
Show that the equation of the axis of symmetry of the graph of f(x) is x = k.
Then , find the value of k if f(x)has a maximum value of 12
superliong 发表于 10-3-2010 04:43 PM 
有两个办法:
一:completing the square
f(x)=-3x^2+6kx+6-3k
=-3(x^2-2kx)+6-3k
=-3[(x-k)^2-k^2]+6-3k
=-3(x-k)^2+3k^2-3k+6
Hence maximum value is at x=k which is also axis of symmetry of the graph of f(x)
If maximum value =12
Then 3k^2-3k+6=12
3k^2-3k-6=0
k^2-k-2=0
(k-2)(k+1)=0
k=-1,2
x=-1,2
二:Differentiation
f(x)=6-3k+6kx-3x^2
f'(x)=6k-6x
Maximum when f'(x)=0
6k-6x=0
k=x,x=k (line of symmetry)
maximum value, f(k)=12
When x=k, 6-3k+6k^2-3k^2=12
3k^2-3k-6=0
k^2-k-2=0
(k-2)(k+1)=0
k=-1,2
x=-1,2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-3-2010 05:58 PM
|
显示全部楼层
回复 193# walrein_lim88
哇,你好厉害哦!!
这是chapter 2 的 , 也可以用differentiation 来解嘢! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-3-2010 07:01 PM
|
显示全部楼层
发表于 10-3-2010 07:01 PM
|
显示全部楼层
回复 194# superliong
可以啊。。。别忘了dy/dx = 0是可以找出MAX/MINIMUM VALUE 的 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-3-2010 11:19 PM
|
显示全部楼层
发表于 22-3-2010 11:19 PM
|
显示全部楼层
1. if the sum of an arithmetic progression, log y+log y^2+log y^3+...+log y^n is given by n(n+1),find the value of y.
2. given that sin x°, 2 cos x° and 2 sin x° are three consecutive terms in an arithemetic progression.find the value of x° in radians.
3.(i) find the sum of all the integers from 1 to 100 that are divisible by 5.
(ii)hence ,find the sum of all the integers from 1 to 100 that are not divisible by
5.
这3题怎样做? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-3-2010 01:01 PM
|
显示全部楼层
发表于 23-3-2010 01:01 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-3-2010 05:29 PM
|
显示全部楼层
发表于 24-3-2010 05:29 PM
|
显示全部楼层
2. given that sin x°, 2 cos x° and 2 sin x° are three consecutive terms in an arithemetic progression.find the value of x° in radians.
2 cos x° - sin x° = 2 sin x° - 2 cos x°
2 cos x° + 2 cos x° = 2 sin x° + sin x°
4 cos x° = 3 sin x°
4/3 = (sin x°)/(cos x°)
tan x° = 4/3
x° = 53.13° = 0.927 rad
walrein兄,那天我做的也是没错咯?!
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-3-2010 09:49 PM
|
显示全部楼层
发表于 24-3-2010 09:49 PM
|
显示全部楼层
回复 dollyeye
walrein_lim88 发表于 23-3-2010 01:01 PM 
这个格式很美.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-3-2010 10:04 PM
|
显示全部楼层
发表于 24-3-2010 10:04 PM
|
显示全部楼层
回复 199# 乙劍真人
什么叫做格式很美??  |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|