|
今天我们先来看下大伙都很熟悉的世界地图,然后研究几个问题:
一、加拿大(1)和美国(2)相比,两者比例大约会是多少?
二、俄罗斯(3)和中国(4)相比,两者比例大约会是多少?
三、格陵兰岛(5)和非洲(绿色圈,6)相比,两者比例大约会是多少?
不出意外,你的目测结果将与事实相去甚远。
制作世界地图的难题 我们知道,地图是人们为了便于研究,根据真实世界的景象和位置关系制成的平面图。对于一个城市、一个地区而言,测绘地图的工作可以做得非常精确;而放大到整个地球的尺度,就会有问题显现出来。
由于地球是个球形,所以在将地球表面的所有国家区域都绘制到地图上时,主要会面临两个问题:
一是要把立体图正面和背面都画出; 二是要把凸出的部分压平在平面图上。
第一个问题比较好理解,也不难解决,第二个问题需要一点点想象力:如果我们要把一个球的表面拉平在一张纸上,少不了得把中间凸出部分压平下去。
而这样的“压平”动作就会产生误差,导致失真。反过来也是一样,用一张平的白纸是无法将一个球的表面完美合缝地覆盖的,小伙伴们试试就知道。
为了解决这两个问题,在地图制图的生产实践中,就出现了“投影”的方法。
简单来说,投影是将球体近似转变成其他形体,再将其进一步展开成为平面图。
常见的投影方式 不同的投影方式决定了不同的投影类型:
一、按照投影后的几何变形,可将投影分为等角、等积和等距投影。
等角投影:投影过程中地面上的任意两条直线的夹角保持不变。等角投影也称为正形投影,是三种几何变形里最常见的一种投影方式。 等积投影:投影过程中地面上的任意区域面积保持不变。 等距投影:投影过程中地面上任意两个点之间的距离保持不变。
这里要注意的是,由于球形的特殊性,它向其他图形的投影过程中不可避免会出现变形和失真,所以几何变形的这三种方式无法兼顾,只能根据实际情况对需要保持精确的要素进行取舍。
换言之,等角投影无法保证等积和等距,等积/等距投影也无法保证等角和等距/等积。
二、 按投影面的形态不同,投影可分为圆锥投影、圆柱投影和方位投影。 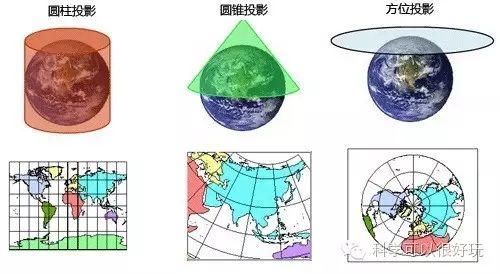
其中圆柱投影是最常见的投影方式,指用一个圆柱体罩住地球,把地表的位置投影到圆体面上,然后将圆柱体侧面切开展成平面。
三、根据投影面与地球的相对位置的不同,投影可分为正轴投影、斜轴投影和横轴投影,其中正轴投影是最常见的方式。
结合上述三种分类方法(几何变形方式、投影面形态、投影面位置),我们可以对不同的投影方式加以命名。如正轴等角圆柱投影(也是最常用的投影方式),斜轴等角圆锥投影方式等。
历史上也有一些投影以设计者的名称命名,其实大多也可归到上述分类里。
其中最著名的投影方式叫做墨卡托投影。
墨卡托投影 墨卡托投影由荷兰地图学家墨卡托(G.Mercator)于1569年创立。它是假想一个与地轴方向一致的圆柱体与地球相切,将经纬网投影到圆柱面上,将圆柱面展为平面后得到的投影。
不明白的小伙伴看这个图:把正放的地球形状外展成圆柱体,再将其侧面展开。
墨卡托投影是影响最大的一种地图投影方法,世界上绝大多数地图(包括google地图和百度地图),都采用的是墨卡托投影(或其升级版本)。
按照前面的分类方式,墨卡托投影属于正轴等角圆柱投影。
根据墨卡托投影的规则,地图上的经线是一组竖直的等距离平行直线,纬线是垂直于经线的一组平行直线,各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等,即没有角度变形。
在地图上保持方向和角度的正确,是墨卡托投影最大的优点。简单来说就是,由于它具有在各个方向上均等扩大的特性,保持了方向和相互位置关系的正确。也就是说如果循着墨卡托投影图上两点间的直线航行,方向不变就可以一直到达目的地。
因此它对船舰在航行中定位、确定航向都具有有利条件,给航空和航海带来了很大方便,故广泛用于编制航海图和航空图。今天,大多数深海航行者依旧使用着使用墨卡托投影制作的航海图。
墨卡托投影的缺陷 正如之前所说,地球是个球体,各种平面投影方式无法对其的所有数据兼顾。
墨卡托投影要保证世界地yey图里方向和角度的正确,就不可避免地导致纬线间的间隔从赤道向两极变形逐渐增大。这也是墨卡托投影的最大缺点:长度和面积和现实差别太大,变形严重。而且纬度越高的地区,长度和面积变形越严重。
比如开头的那三个问题:
 一、加拿大(1)和美国(2)相比,两者比例大约会是多少? 从图上看,加拿大是个很高的长方形,目测其面积接近美国(本土加阿拉斯加)的两倍,至少也有1.3~1.5倍。
而实际上,加拿大不仅扭曲得不像样,而且还被放大了好几倍。它其实是个类似正方形的形状,比美国大不了多少:加拿大面积是998万平方千米,美国两部分合起来约963万平方千米,998÷963≈1.04,加拿大只比美国本土加阿拉斯加大了4%。
 二、俄罗斯(3)和中国(4)相比,两者比例大约会是多少? 从图上看,俄罗斯南北方向的宽度和中国几乎差不多,而东西方向的长度几乎是中国的2.5倍,所以目测俄罗斯面积得有中国的2.5倍以上。
实际情况是俄罗斯确实很大,但也没有辣么大。因为它的纬度高,所以墨卡托投影变形要比中国严重得多。俄罗斯面积为1709.82万平方千米,我国土地面积是960万平方千米,1709.82÷960≈1.78,大了1倍都不到。
 三、格陵兰岛(5)和非洲(绿色圈,6)相比,两者比例大约会是多少? 在墨卡托投影的地图上,除了南北极之外,变形最严重的非格陵兰岛莫属。根据目测,格陵兰岛似乎得有小半个非洲大。换句话说,如果我们用图里的格陵兰岛去填非洲,两个格陵兰岛再多一点点感觉就填满了,应该放不下三个。
而如果计算一下的话:非洲面积约为3020万平方千米,格陵兰岛面积是217万平方千米,3020÷217≈13.9。非洲的面积接近格陵兰岛的14倍!
想不到吧。
三个例子形象地说明,墨卡托投影最大问题是高纬地区的长度和面积严重失真。
不过对于南北极而言,这个问题反而并不麻烦:因为圆柱投影的展开图本来就展示不了圆柱的顶面和底面,所以一般的正式地图里都会把两极绘制出来单独展示的:
地图知识番外篇 除了今天的墨卡托主题之外,还有一个关于地图的小知识:世界上各个国家在绘制地图的时候,会倾向于选择把自己国家放在地图的中心(或靠近中心)的位置,并以此为基础来绘制其他国家的位置。
这就是为什么在中国我们会看到大部分世界地图长成这样:
而在欧洲和中东的大多数国家里,世界地图会长成这样:
所以有种说法是,日本人初次到英国看地图时,十有八九都会看晕:因为他们会习惯性地以为地图中心的那个岛还是自己的岛,但周围的地形他们却一点都不熟悉!
|