|
|
|
If @i+3j and 3i+(8+@)j are two parallel vector , find the possible value of @. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-2-2005 09:45 PM
|
显示全部楼层
|
ABCD is a quadrilateral. P,Q,R and S are mid-point of AB,BC,CD and DA respectively.Prove that PQRS is a parallelogram? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-2-2005 04:10 PM
|
显示全部楼层
发表于 24-2-2005 04:10 PM
|
显示全部楼层
Hust 于 23-2-2005 09:42 PM 说 :
If @i+3j and 3i+(8+@)j are two parallel vector , find the possible value of @.
@i+3j=k{3i+(8+@)j} because they are parallel vector
@i+3j=3ki+(8k+@k)j
@=3k 3=8k+@k
k=@/3
3=8(@/3)+@(@/3)
9=8@+@^2
@^2+8@-9=0
(@+9)(@-1)=0
@=-9 or @=1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-2-2005 04:23 PM
|
显示全部楼层
发表于 24-2-2005 04:23 PM
|
显示全部楼层
Hust 于 23-2-2005 09:45 PM 说 :
ABCD is a quadrilateral. P,Q,R and S are mid-point of AB,BC,CD and DA respectively.Prove that PQRS is a parallelogram?
我不会post diagram 出来,你画了图画才看解答吧!
let the position vector of A,B,C,D be a,b,c,d
i.e:OA=a,OB=b,OC=c,OD=d
S is a mid point of AD
OP={OA+OD}/2
=1/2(a+d)
P is a mid point of AB
OP=(OA+OB)/2
=1/2(a+b)
Q is a mid point of BC
OQ=(OB+OC)/2
=1/2(b+c)
R is a mid point of CD
OR=(OC+OD)/2
=1/2(c+d)
SP=SO+OP
=-1/2(a+d)+1/2(a+b)
=1/2(b-d)
RQ=RO+OQ
=-1/2(c+d)+1/2(b+c)
=1/2(b-d)
vectorSP=vectorRQ
SP=RQ
SP parallel RQ
therefore,SPRQ is a parallelgram |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-2-2005 09:06 PM
|
显示全部楼层
我有数学的疑惑
Using the vector method , prove that the perpendicular bisectors of the sides of a triangle are convergent. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-2-2005 09:13 PM
|
显示全部楼层
|
Prove that the diagonals of a rhombus are perpendicular? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-2-2005 10:35 PM
|
显示全部楼层
发表于 26-2-2005 10:35 PM
|
显示全部楼层
Hust 于 25-2-2005 09:13 PM 说 :
Prove that the diagonals of a rhombus are perpendicular?
let OABC is a rhombus with dot OA=a,dot OB=b
from triangle OAB,dot AB=b-a
from triangle OBC,dotOC=a+b
hence,dot(AB.OC)=(b-a)(a+b)
=b.a+b.b-a.a-a.b
=|b|^2-|a|^2
=0 because |a|=|b| in a rhombus |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 27-2-2005 10:35 AM
|
显示全部楼层
|
Find the probability of throwing three sixes twice in five throws of six dice? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-2-2005 07:39 PM
|
显示全部楼层
发表于 27-2-2005 07:39 PM
|
显示全部楼层
|
A,B,c are the vertices of a triangle.The perpendicular line from A to BC and the perpendicular line from B to AC meet at D.Show that CD is perpendicular to AB. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-2-2005 02:11 PM
|
显示全部楼层
发表于 28-2-2005 02:11 PM
|
显示全部楼层
Leong13 于 27-2-2005 07:39 PM 说 :
A,B,c are the vertices of a triangle.The perpendicular line from A to BC and the perpendicular line from B to AC meet at D.Show that CD is perpendicular to AB.
∠AGD = ∠DFB = 90
∠ADG =∠FDB
所以 ∠GAD =∠ DBF
给一个四方形, 内角的合为360度。
所以∠GAE+ ∠GDE = 180
∠GDE= ∠CDB
所以 ∠GAE=∠GAD +∠DAE
=∠DCF+∠DBF
∠GAD =∠ DBF,
所以 ∠DAE =∠ DCF.
---> ∠DAE =∠ DCF.∠ADE =∠CDF,
SO,∠AED =∠ DFC = 90.
CD is perpendicular to AB
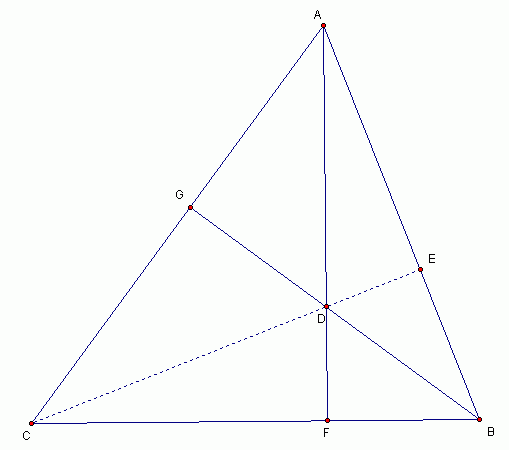
[ Last edited by fritlizt on 28-2-2005 at 02:13 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-3-2005 02:20 PM
|
显示全部楼层
发表于 1-3-2005 02:20 PM
|
显示全部楼层
数学的疑惑
1.An aircraft that has a speed of 350kmh-in still air is heading south.The velocity of the wind from the north-east direction is 50kmh- .Determine the resultant velocity of thr aircrafy.
2.A force of 7N and a force P has a resultant force of magnitude 15N.Find P if the angle between the two forces is
(a)90sudut (b)60sudut. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-3-2005 12:21 PM
|
显示全部楼层
发表于 10-3-2005 12:21 PM
|
显示全部楼层
Hust 于 27-2-2005 10:35 AM 说 :
Find the probability of throwing three sixes twice in five throws of six dice?
6個中出現3個6的機率
(A,B,C,D,E,F) 中
A 代表第一個出現的數字
B 代表第二個出現的數字
C 代表第三個出現的數字
D 代表第四個出現的數字
E 代表第五個出現的數字
F 代表第六個出現的數字
3個6可以有以下的組合 :
3個6和其他三個數字組成
3個6和其他兩個數字組成
3個6和其他一個數字組成
(6,6,6,A,B,C)的組合可能 10
(6,6,6,A,B,C)的排列可能 120
(6,6,6,A,B,C)共形成1200種三個6和三個不同的數字組合的可能
解說:
A,B,C 可以有 10 種組合 (5C3)
(6,6,6,A,B,C) 可以有 120 種排列 (6P6 / 3P3)
每個不同的組合,各自有120種排列
(6,6,6,A,A,B)的組合可能 20
(6,6,6,A,A,B)的排列可能 60
(6,6,6,A,A,B)共形成1200種三個6和兩個不同的數字組合的可能
解說:
A,B 可以有 20 種組合 (5C1) * (4C1)
先選出一個數字A,再選出另外一個數字B
(6,6,6,A,A,B) 可以有 60 種排列 (6P6 / 3P3 / 2P2)
每個不同的組合,各自有60種排列
(6,6,6,A,A,A)的組合可能 5
(6,6,6,A,A,A)的排列可能 20
(6,6,6,A,A,A)共形成100種三個6和一個不同的數字組合的可能
解說:
A 可以有 5種組合
(6,6,6,A,A,A) 可以有 20 種排列 (6P6 / 3P3 / 3P3)
每個不同的組合,各自有20種排列
三個六的可能 = 1200 + 1200 + 100 = 2500種
六個數的可能 = 6 x 6 x 6 x 6 x 6 x 6 = 46656種
六個數字中出現三個六的機率 = 2500 / 46656
用隨機程式演算過,46656次中出現3個6的次數為 2500左右
所以答案絕對正確    |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|