|
|
 发表于 23-10-2004 04:45 PM
|
显示全部楼层
发表于 23-10-2004 04:45 PM
|
显示全部楼层
23/10/2004,星期六
高中(B30)
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-10-2004 10:13 AM
|
显示全部楼层
发表于 24-10-2004 10:13 AM
|
显示全部楼层
∵a+b>c
∴(a+b)/c>1
顯燃(a+b)/c的最小值為1,是錯誤的! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-10-2004 12:10 PM
|
显示全部楼层
发表于 24-10-2004 12:10 PM
|
显示全部楼层
当 tita 趋进 0
(a+b)/c 趋进 1
(a+b)/c 的 range 是 ( 1,√2 ]
[ Last edited by 多普勒效应 on 24-10-2004 at 12:11 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-10-2004 10:34 AM
|
显示全部楼层
发表于 25-10-2004 10:34 AM
|
显示全部楼层
25/10/2004,星期一
初中(A31)
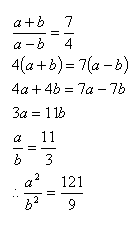 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-10-2004 01:48 PM
|
显示全部楼层
发表于 25-10-2004 01:48 PM
|
显示全部楼层
∵(a+b)/(a-b) = 7/4
利用合分比性質
∴〔(a+b)+(a-b)〕/〔(a+b)-(a-b)〕=(7+4)/(7-4)
則a/b=11/3
故(a^2)/(b^2) 之值為121/9。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-10-2004 10:31 AM
|
显示全部楼层
发表于 26-10-2004 10:31 AM
|
显示全部楼层
已知 六位数 174xyz 能被 7,11,13 整除。
所以 六位数 174xyz 必能被 7,11,13的最小公倍數1001 整除。
顯然 六位数 174xyz ÷1001=174
則 x=1,y=7,z=4。
故 x + y + z=12 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-10-2004 01:32 PM
|
显示全部楼层
发表于 26-10-2004 01:32 PM
|
显示全部楼层
26/10/2004,星期二
初中(A32) 已知 六位数 174xyz 能被 7,11,13 整除。
求 x + y + z 。 (待解)
7, 11, 13 的 GSTK 是 1001。
所以 174xyz 应该是 1001 的倍数。
所以 174xyz 只有 1001 x 174 = 174174
那么, x + y + z = 1 + 7 + 4 = 12 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-10-2004 11:47 AM
|
显示全部楼层
发表于 27-10-2004 11:47 AM
|
显示全部楼层
27/10/2004,星期三
初中(A33)
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-10-2004 07:02 PM
|
显示全部楼层
发表于 27-10-2004 07:02 PM
|
显示全部楼层
設x為(n-1)位數,n>1
(10^n+10x+1)-x=13439
x=(13438-10^n)/9>0
則n<5
(1)若n=2,則x=1482(不合)
(2)若n=3,則x=1382(不合)
(3)若n=4,則x=382 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-10-2004 08:16 AM
|
显示全部楼层
发表于 28-10-2004 08:16 AM
|
显示全部楼层
27/10/2004,星期三
初中(A33) 在某一数,x 的前后各添上"1"。
得到的数 y, 比 x 大 13439。
求 x 。
以愚蠢的方法做。。 ^_^
x 前后添 1 , 那么就是 1"x"1
y - x = 13439
1"x"1
- "x"
--------- ==> x 应该是3位数, abc
13439
---------
所以 1 a b c 1
- a b c
--------------
1 3 4 3 9
--------------
以最快方法添进去,
c = (1)1 - 9 = 2 (1,需要借位)
b = (1)2 - *1* - 3 = 8 (1,需要借位 / *1* 被借位)
a = 8 - *1* - 4 = 3
x = 382
酱比较快, 我觉得。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-10-2004 09:14 PM
|
显示全部楼层
发表于 28-10-2004 09:14 PM
|
显示全部楼层
(1)若a=1
則9 < b^2 < 27
即3 < b < 6
∴b=4,5
(2)若a=2
則6 < b^2 < 24
即2 < b < 5
∴b=3,4
(3)若a=3
則1 < b^2 < 17
即1 < b < 5
∴b=2,3,4
(4)若a=4
則0 < b^2 < 12
即0 < b < 4
∴b=1,2,3,4
(5)若a=5
則0 < b^2 < 3
即0 < b < 2
∴b=1
故共有12組 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-10-2004 09:25 AM
|
显示全部楼层
发表于 30-10-2004 09:25 AM
|
显示全部楼层
03/10/2004,星期日
大专(C7)
用 geometric progression ,Sn = a( r^n -1 )
r -1
既 a = 1, r = 2, n = x
1(2^× -1) = 2^× -1 = 1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)
2 -1
(2^× -1) = [1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)]
x x
得知 arithmetic mean > geometric mean
既 [ 1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)]/x > [1 x 2 x 2^2 x 2^3 x…x 2^(×-1)]^ 1/x
= [2^(0 + 1 + 2 + 3 +…+ x-1)]^ 1/ x
= [2 ^(x(x-1) / 2)]^1/ x
= 2^[ (x-1) / 2]
(2^× -1) /x > 2^[ (x-1) / 2]
[(2^× -1) /x]^1/(x-1) > {2^[ (x-1) / 2]}^1/(x-1)
= 2^1/2
> 1
(2^× -1) /x = [1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)]/x
< [2^(x-1) + 2^(x-1) + 2^(x-1) +...+ 2^(x-1)]/x
= x(2^(x-1))/x
= 2^(x-1)
[(2^× -1) /x]^1/(x-1) < [2^(x-1)]^1/(x-1)
= 2
1 < [(2^x -1) /x]^1/(x-1) < 2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-10-2004 09:43 AM
|
显示全部楼层
发表于 30-10-2004 09:43 AM
|
显示全部楼层
29/10/2004,星期五
高中(B32) (B32) 若 f(x) = (x-1)(x-2)(x-3)(x-4)…(x-10),
求 f '(10)。
f(x) =(x-1)(x-2)(x-3)(x-4)…(x-10)
f(10) =(10-1)(10-2)(10-3)(10-4)…(10-10)
= 0
f'(10)= 0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-10-2004 02:13 PM
|
显示全部楼层
发表于 30-10-2004 02:13 PM
|
显示全部楼层
ah_mok 于 30-10-2004 09:43 AM 说 :
29/10/2004,星期五
高中(B32) (B32) 若 f(x) = (x-1)(x-2)(x-3)(x-4)…(x-10),
求 f '(10)。
f(x) =(x-1)(x-2)(x-3)(x-4)…(x-10)
f(10) =(10-1)(10-2)(10-3)(10-4)…(10-10)
= 0
...
对不起,对不起!!
早上睡不清醒。。。乱写了一通!!
答案该是
假设g(x) = (x-1)(x-2)(x-3)(x-4)…(x-9)
h(x) = (x-10)
f(x) = g(x)h(x)
f '(x) = g'(x)h(X)+g(x)h'(x)
= g'(x)(x-10) + g(x)(1)
f'(10) =g'(10)(10-10) + g(10)
= g(10)
=(10-1)(10-2)(10-3)(10-4)…(10-9)
=9(8)(7)(6)(5)(4)(3)(2)(1)
=362880
对不起,对不起!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-10-2004 03:14 PM
|
显示全部楼层
发表于 30-10-2004 03:14 PM
|
显示全部楼层
已知 x, y 为正整数,且 (x,y) 满足 1/x + 1/y = 1/30 。
求 y 的极大值。
∵1/x + 1/y = 1/30 。
去分母 30y+30x=xy
xy-30x-30y=0
x(y-30)-30(y-30)=900
(x-30)(y-30)=900
當x-30=1時,y-30有極大值900
故y的極大值為930 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:46 PM
|
显示全部楼层
430201 于 28-10-2004 09:14 PM 说 :
(1)若a=1
...
(4)若a=4
則0 < b^2 < 12
即0 < b < 4
∴b=1,2,3,4
...
故共有12組
错了!! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 09:55 PM
|
显示全部楼层
ah_mok 于 30-10-2004 09:25 AM 说 :
03/10/2004,星期日
大专(C7)
用 geometric progression ,Sn = a( r^n -1 )
r -1
既 a = 1, r = 2, n = x
1(2^× -1) = 2^× -1 = 1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)
2 -1
(2^× -1) = [1 + 2 + 2^2 + 2^3 +…+ 2^(×-1)]
x x
这方法只考虑到 x 为某正整数。。。
不够全面!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 31-10-2004 05:14 PM
|
显示全部楼层
发表于 31-10-2004 05:14 PM
|
显示全部楼层
【忙中有錯,該打屁屁】
(1)若a=1
則9 < b^2 < 27
即3 < b < 6
∴b=4,5
(2)若a=2
則6 < b^2 < 24
即2 < b < 5
∴b=3,4
(3)若a=3
則1 < b^2 < 17
即1 < b < 5
∴b=2,3,4
(4)若a=4
則0 < b^2 < 12
即0 < b < 4
∴b=1,2,3
(5)若a=5
則0 < b^2 < 3
即0 < b < 2
∴b=1
故共有11組 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|