STPM-学校功课討論区

~HeBe~_@

[ 本帖最后由 ~HeBe~_@ 于 12-7-2008 12:19 PM 编辑 ]

darksider

The quadratic equation 2x^2 + ax + 3 = 0 , x^2 + bx +6=0 , with a and b as constants , have a common root. Show that 2a^2 + 2b^2 -5ab + 27 = 0

Given that f(x) = x^n - nx + n - 1 for integer n>1 . By considering f(x) and f'(x) , show that f(x) = (x-1)^2 g(x) where g(x) is a function with integer coefficients.

Hence, show that 3^2n - 8n -1 is divisible by 64 for integer n>1

[ 本帖最后由 darksider 于 4-7-2008 10:54 PM 编辑 ]

woun

原帖由 darksider 于 4-7-2008 06:30 PM 发表
The quadratic equation 2x^2 + ax + 3 = 0 , x^2 + bx +6 , with a and b as constants , have a common root. Show that 2a^2 + 2b^2 -5ab + 27 = 0

Given that f(x) = x^n - nx + n - 1 for integer n>1 . By  ...

这是equation 吗？

darksider

对，我忘了放＝0，谢谢！

mathlim

原帖由 darksider 于 4-7-2008 06:30 PM 发表
The quadratic equation 2x^2 + ax + 3 = 0 , x^2 + bx +6=0 , with a and b as constants , have a common root. Show that 2a^2 + 2b^2 -5ab + 27 = 0

设α是公共解。
2α^2 + aα + 3 = 0  ——(1)
α^2 + bα +6=0 ——(2)
(1) - (2)×2
(a-2b)α - 9 = 0
α = 9/(a-2b)
代入 (2)
[9/(a-2b)]^2 + b[9/(a-2b)] + 6 = 0
81 + 9b(a-2b) + 6(a^2-4ab+b^2) = 0
81 + 9ab - 18b^2 + 6a^2 - 24ab + 24b^2 = 0
6a^2 + 6b^2 - 15ab + 81 = 0
2a^2 + 2b^2 - 5ab + 27 = 0

mathlim

原帖由 darksider 于 4-7-2008 06:30 PM 发表
Given that f(x) = x^n - nx + n - 1 for integer n>1 . By considering f(x) and f'(x) , show that f(x) = (x-1)^2 g(x) where g(x) is a function with integer coefficients.
Hence, show that 3^2n - 8n -1 is divisible by 64 for integer n>1

f(x) = x^n - nx + n - 1
f'(x) = nx^(n-1) - n
f(1) = 1 - n + n - 1 = 0
f'(1) = n - n = 0
∴ f(x) = (x-1)^2 g(x)

令x = 9
f(9) = (9-1)^2 g(9)
9^n - 9n + n - 1 = 64 g(9)
3^2n - 8n - 1 = 64 g(9)
∴ 3^2n - 8n -1 可以被 64 整除，n > 1

darksider

謝謝！
這里又一題inequality的
Sketch on the same diagram , the graphs of y = |x-3|+|x+3| and y = 2/7 (x+24)
Hence , find the solution set of the inequality 7[ |x-3| + |x+3|] > 2(x+24)

不死的ProG

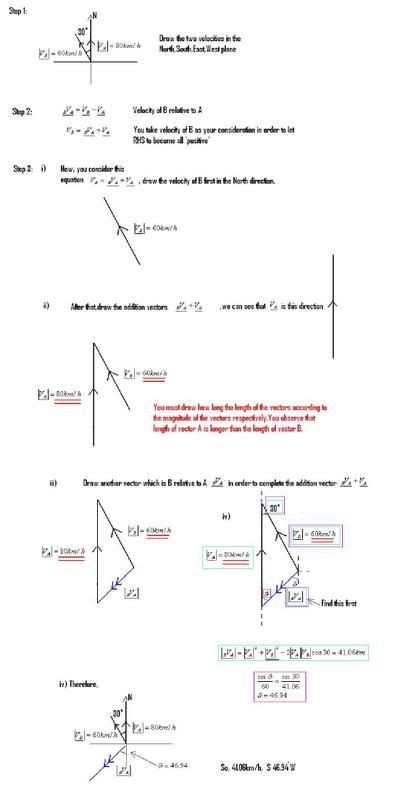
我的vector快死了

a lane crosses with another lane at O an angle of 60‘。a boy, A, is 300m from O in one of the lanes and another boy, B, is 400m from O in another lane. Both the boys run towards O simultaneously, with A moving at a speed of 15km/h and B at a speed of 12km/h. Find the closest distance between A & B. (ans : 151m)


ABCD is a square with M and N as mid-points of BC and CD respectively. If m = AM and n = AN, express AB, AC and BD in terms of m and n.
(ans : 2/3(2m-n) , 2/3(m+n), 2(n-m))

mathlim

原帖由 不死的ProG 于 10-7-2008 12:40 AM 发表
ABCD is a square with M and N as mid-points of BC and CD respectively. If m = AM and n = AN, express AB, AC and BD in terms of m and n.
(ans : 2/3(2m-n) , 2/3(m+n), 2(n-m))

我想提供一个比较麻烦，但是比较容易掌握的方法。希望能帮到你。

设AB = x, AD = y

m = x + y/2 ——(1)
n = x/2 + y ——(2)

(1)×2 - (2)
x = (2/3)(2m – n)

(2)×2 - (1)
y = (2/3)(2n – m)

∴ AB = x = (2/3)(2m – n),

AC = x + y = (2/3)(2m – n) + (2/3)(2n – m) = (2/3)(m + n),

BD = y - x = (2/3)(2n – m) - (2/3)(2m – n) = 2(n - m)

mathlim

原帖由 不死的ProG 于 10-7-2008 12:40 AM 发表
a lane crosses with another lane at O an angle of 60‘。a boy, A, is 300m from O in one of the lanes and another boy, B, is 400m from O in another lane. Both the boys run towards O simultaneously, with A moving at a speed of 15km/h and B at a speed of 12km/h. Find the closest distance between A & B. (ans : 151m)

OA = 0.3 – 15t
OB = 0.4 – 12t
AB² = OA² + OB² – 2OA×OBcos60°
AB² = 225t² – 9t + 0.09 + 144t² – 9.6t + 0.16 – 180t² + 9.6t – 0.12
= 189t² – 9t + 0.13
= 189(t – 1/42)² + 4/175

∴ the closest distance between A & B is √(4/175) ≈ 0.151km = 151m.

~HeBe~_@

~HeBe~_@

这种题目要画graph才看到的。。

darksider

原帖由 ~HeBe~_@ 于 2008/7/13 02:05 AM 发表
这种题目要画graph才看到的。。

明白了，謝謝

Show that the roots of the quadratic equation ax^2 + bx + c = 0 are given by (QUADRATIC FORMULA)

i) Deduce that if m + ni , where m, n subset R , is a root of the quadraticeqaution , then the other root is m- ni...

不會做 i) 的部分.

mathlim

原帖由 darksider 于 14-7-2008 04:12 PM 发表
Show that the roots of the quadratic equation ax^2 + bx + c = 0 are given by (QUADRATIC FORMULA)
i) Deduce that if m + ni , where m, n subset R , is a root of the quadraticeqaution , then the other root is m- ni...

设 f(x) = ax² + bx + c, a, b, c ∈R.
z = m + ni, z = m - ni
f(z) = 0
az² + bz + c = 0
az² + bz + c = 0
az² + bz + c = 0
a z² + b z + c = 0
a (z)² + b z + c = 0
f(z) = 0

darksider

原帖由 mathlim 于 2008/7/15 12:25 PM 发表


设 f(x) = ax² + bx + c, a, b, c ∈R.
z = m + ni, z = m - ni
f(z) = 0
az² + bz + c = 0
az² + bz + c = 0
az² + bz + c = 0
a z² + b z + c = 0
a (z)² + b z + c = 0 ...

那個underline的部分我可以用 * 來代替嗎？
謝謝你！

mathlim

我的课本的符号，横线是在上面的。
Z = x + yi
_
Z = x - yi

darksider

For each of the following functions determine if it has the same sign for all values of x , and in such case , state its sign.

f(x) = 3x^2 - 7x + 5
g(x) = 5 + 4x - x^2

那个 "sign" 是什么意思？是不是指 positive / negative?

hamilan911

是的
将它completing the square就解决了

mathlim

原帖由 darksider 于 20-7-2008 08:21 PM 发表
For each of the following functions determine if it has the same sign for all values of x , and in such case , state its sign.
f(x) = 3x^2 - 7x + 5
g(x) = 5 + 4x - x^2

f(x) = ax² + bx + c

1) 如果 a ＞ 0 且 b² - 4ac ＜ 0, 则 f(x) ＞ 0;
2) 如果 a ＞ 0 且 b² - 4ac = 0, 则 f(x) ≥ 0;
3) 如果 a ＜ 0 且 b² - 4ac ＜ 0, 则 f(x) ＜ 0;
4) 如果 a ＜ 0 且 b² - 4ac = 0, 则 f(x) ≤ 0.

那个sign是指f(x)的sign. (positive / negative)

darksider

谢谢 ：）

再来一题
15a) Find the range of values of the expression 5x^2 -200x + 1969 as x changes between 0 and 50 inclusive.
                   不懂怎样开始...

b) Find , in terms of a and b , the range set of values for t such that 3t^2 + 6at >= 4b^2 - 3a^2 where a,b are given positive numbers.

[ 本帖最后由 darksider 于 22-7-2008 09:45 PM 编辑 ]