University-数学讨论区-Calculus, Real Analysis

~HeBe~_@

对不起，粗心又来了。。。

~HeBe~_@

9）
首先用substitution,Let u = a^2 + x^2
然后∫  u^2 / (u^2 - a^2)  dx = .......

然后再用substitution , Let v = a^2 + u^2
然后 ∫  a^2 / (v^2 - a^2)  dx = ....


最后所找到的答案in term of v，把他换回in term of u , 再换回in term of x.

∫ [√ (a^2 + x^2)]/x dx =  √(a^2 + x^2) - a ln |  [a+ √ (a^2 + x^2)]/x   | + c

DADDY_MUMMY

原帖由 ~HeBe~_@ 于 27-1-2008 03:30 PM 发表
9）
首先用substitution,Let u = a^2 + x^2
然后∫  u^2 / (u^2 - a^2)  dx = .......

然后再用substitution , Let v = a^2 + u^2
然后 ∫  a^2 / (v^2 - a^2)  dx = ....


最后所找到的答案in term of v ...

1)Prove ∫ (sec x) ^n dx = [tan x (sec x) ^ (n -2)]/ (n – 1) +
                                     [(n – 2)/ (n – 1)] *∫ (sec x) ^ (n -2) dx
然后,这个ne?

DADDY_MUMMY

天啊！好多蜘蛛网啊！

~HeBe~_@

为什么说好多蜘蛛网哦？

DADDY_MUMMY

这里好像冷清清的～～～
没什么人上来这儿～～～
当然！你我都是人！

TCLGT

怎样 int(e^x lnx) dx

dunwan2tellu

原帖由 TCLGT 于 29-1-2008 10:54 PM 发表
怎样 int(e^x lnx) dx

int(e^x lnx)dx = e^x ln x - int(e^x / x) dx

e^x = 1 + x + x^2/2 + x^3/3! + .... (用 e^x 的 power series)

e^x/x = 1/x + sum_(k=1 to infity) (x^(k-1)/k!)

int(e^x/x) = ln x + sum_(k=1 to infity) (x^k/(k.k!))

int(e^x lnx)dx = e^x ln x + ln x + sum_(k=1 to infity) (x^k/(k.k!))

[ 本帖最后由 dunwan2tellu 于 1-2-2008 10:40 PM 编辑 ]

dunwan2tellu

原帖由 DADDY_MUMMY 于 28-1-2008 12:39 PM 发表

1)Prove ∫ (sec x) ^n dx = [tan x (sec x) ^ (n -2)]/ (n – 1) +
                                     [(n – 2)/ (n – 1)] *∫ (sec x) ^ (n -2) dx
然后,这个ne?

(sec x)^n = (sec x)^(n-2) * (sec x)^2= (sec x)^(n-2) * (tan^2 x + 1)
               = tan^2 x * (sec x)^(n-2) + (sec x)^(n-2)

int ( tan^2 x *(sec x)^(n-2))dx = int ( tan x * (tan x * sec x) * (sec x)^(n-3) ) dx
                                                 = tan x * 1/(n-2) * (sec x)^(n-2) - int ( (sec x)^2 * 1/(n-2) * (sec x)^(n-2)) dx
(用 integration by parts on (tan x * sec x) * (sec x)^(n-3) 和 tan x)

之后就 simplify

DADDY_MUMMY

Let P be an interior point of an equilateral triangle ABC such that (AP^2)=(BP^2)+(CP^2). Prove that angle BPC = 150 degrees.

dunwan2tellu

原帖由 DADDY_MUMMY 于 15-2-2008 09:02 PM 发表
Let P be an interior point of an equilateral triangle ABC such that (AP^2)=(BP^2)+(CP^2). Prove that angle BPC = 150 degrees.

Let A(1,sqrt[3]) , B(0,0) , C(2,0) ,P(x,y) .

=> (x-1)^2 + (y-sqrt[3])^2 = x^2 + y^2 + (x-2)^2 + y^2

=> x^2 - 2x + y^2 + 2sqrt[3] y = 0

=> (x-1)^2 + (y+sqrt[3])^2 = 4

P = 圆形轨迹，圆心 (1,-sqrt[3]) ,半径 = 2 ，在 ABC 里面。

设 Q(1,-sqrt[3]) , 那么 QBC = 等边三角形 = ABC , 所以 minor <BQC = <BAC = 60

=> major <BQC = 300

=> <BPC = 1/2 * major < BQC = 150 (angle at center is double the angle at circumference)

p/s : Calculus 题目？？

ENSEN_1212

write down an expression, in terms of n, for the n^th term of each of of these sequences.

1) 1,2,1,2,1,2,1,2,......1,2,1,2....

2) 1,2,3,1,2,3,1,2,3......1,2,3,1,2,3.....

详圣

原帖由 ENSEN_1212 于 19-2-2008 10:25 PM 发表
write down an expression, in terms of n, for the n^th term of each of of these sequences.

1) 1,2,1,2,1,2,1,2,......1,2,1,2....

2) 1,2,3,1,2,3,1,2,3......1,2,3,1,2,3.....

1) 1 + (1 + (-1)^n)/2

2) 1+  [1 + (-1)^(n mod 3)]/2 + 0^(n mod 3) , 0 <= n mod 3 <= 2

多普勒效应

试一试这题 ^^
不会很难,不过看起来满特别:

多普勒效应

原帖由 ENSEN_1212 于 19-2-2008 10:25 PM 发表
write down an expression, in terms of n, for the n^th term of each of of these sequences.

1) 1,2,1,2,1,2,1,2,......1,2,1,2....

也可以这样表示:
1.  an =
               

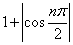
2.  an = 1 + 3[k/3]   , [x]  是小于 x 的最大整数.

[ 本帖最后由 多普勒效应 于 12-3-2008 07:11 PM 编辑 ]

~HeBe~_@

To prove lim n->inf  X_n = x/2

Proof:  

lim n->inf  X_n = lim n->inf        ([x]+[2X]+...+[nx])/n^2
                        = lim n->inf      ( (n/2) ([X] +[nX]) )/ n^2                         <= sum to n
                        = lim n->inf      (1/2n) ([X] +[nX])      <= use L'Hospital Rules
                        = lim n->inf      (1 + X)/2                  to get this
                        =   1/2 +X/2

为什么我得不到X/2 ???

TCLGT

原帖由 ~HeBe~_@ 于 12-3-2008 07:22 PM 发表
To prove lim n->inf  X_n = x/2

Proof:  

To prove lim n->inf  X_n = x/2

Proof:  

lim n->inf  X_n = lim n->inf        ([x]+[2X]+...+[nx])/n^2
                        = lim n->inf      ( (n/2) ([X] +[nX]) )/ n^2                         <= sum to n
                        = lim n->inf      (1/2n) ([X] +[nX])      <= use L'Hospital Rules
                        = lim n->inf      (1 + X)/2                  to get this
                        =   1/2 +X/2                       ...

应该是
lim n->inf      (1/n + X)/2
所以 X/2

~HeBe~_@

Proof:  

lim n->inf  X_n = lim n->inf        ([x]+[2X]+...+[nx])/n^2
                        = lim n->inf      ( (n/2) ([X] +[nX]) )/ n^2                         <= sum to n
                        = lim n->inf      (1/2n) ([X] +[nX])     
                        =  lim n->inf      (1/2n) [X] +  (1/2n)  [nX]     <= use L'Hospital Rules
                        = lim n->inf       [x] /2                                   <=  to get this
                        =   X/2

我想应该对了吧~

DADDY_MUMMY

找volume总共有多少种方法？

多普勒效应

原帖由 ~HeBe~_@ 于 13-3-2008 12:33 AM 发表
Proof:  

lim n->inf  X_n = lim n->inf        ([x]+[2X]+...+[nx])/n^2
                        = lim n->inf      ( (n/2) ([X] +[nX]) )/ n^2                         inf      (1/2n) ([X] +[nX])     
...

[x]+[2x]+...+[nx] = (n/2)([x] + [nx]) 这个关系好像不对
反例: n = 3, x = 1.5

[x]+[2x]+[3x] = [1.5] + [3] + [4.5] = 8
但 n([x] +[3x])/2 = 3 (1 + 4)/2 = 7.5!

emm, { [x], [2x], ... [nx] } 未必是等差数列!

[ 本帖最后由 多普勒效应 于 14-3-2008 07:03 PM 编辑 ]