几何问题

fritlizt

pipi 于 27-9-2004 09:28 AM  说 :
之前讨论的那一题，我猜我得到了它一般性的答案吧！！
即找到了 f(λ)。
暂时先不公布答案，让大家再试试。
至于原题的答案（当 λ＝2），是 1/7 吧！！
（如果这答案不对，那我那一般性的答案也就错了 ...

没错，当λ＝2，答案是1/7。
当λ＝3 的时候，你的答案会是什么呢？？
f(λ) 你先不要公布，我也想找看， 看看答案是否一样。

[ Last edited by fritlizt on 27-9-2004 at 12:00 PM ]

pipi

当λ＝3 的时候，f(λ) ＝ 4/13

pipi

来玩玩这题：

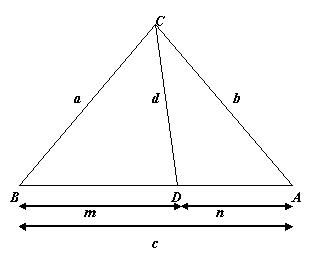
如图，试证明：
(a^2)n + (b^2)m = c(d^2) + cmn

fritlizt

pipi 于 27-9-2004 12:38 PM  说 :
当λ＝3 的时候，f(λ) ＝ 4/13

看来你的一般性答案对了。。。。。

BINGO!

pipi 于 29-9-2004 02:49 PM  说 :
来玩玩这题：

如图，试证明：
(a^2)n + (b^2)m = c(d^2) + cmn

設∠ACD = α﹐∠BCD = β
正弦定理﹐
     a/(sin A) = b/(sin B) = c/(sin C)
=>  sin A = a(sin C)/c , sin B = b(sin C)/c
      n/(sin α) = d/(sin A)
=>  sin α = na(sin C)/cd
      m/(sin β) = d/(sin B)
=>  sin β = mb(sin C)/cd

余弦定理﹐
cos α = (b^2 + d^2 – n^2)/2bd
cos β = (a^2 + d^2 – m^2)/2ad

sin C = sin (α+β)
      = (sin α)(cos β) + (cos α)(sin β)
      = [na(sin C)/cd][ (a^2 + d^2 – m^2)/2ad]
         + [(b^2 + d^2 – n^2)/2bd][mb(sin C)/cd]
2c(d^2) = [(a^2)n + (d^2)n – (m^2)n] + [(b^2)m + (d^2)m – (n^2)m]
        = (a^2)n + (b^2)m + [(d^2) – mn](m+n)       [因為 m+n=c]

故(a^2)n + (b^2)m = c(d^2) + cmn

pipi

sinchee 于 1-10-2004 11:53 PM  说 :
設∠ACD = α﹐∠BCD = β
正弦定理﹐
     a/(sin A) = b/(sin B) = c/(sin C)
=>  sin A = a(sin C)/c , sin B = b(sin C)/c
      n/(sin α) = d/(sin A)
...

余弦定理﹐
cos α = (b^2 + d^2 – n^2)/2bd
cos β = (a^2 + d^2 – m^2)/2ad
...

故(a^2)n + (b^2)m = c(d^2) + cmn

我的做法只用 余弦定理。。。

面积 ADE ：面积 ABE＝DE：BE＝面积 DCE： 面积 BCE

pipi

430201 于 14-10-2004 04:03 PM  说 :
面积 ADE ：面积 ABE＝DE：BE＝面积 DCE： 面积 BCE

这是哪一题？？

pipi

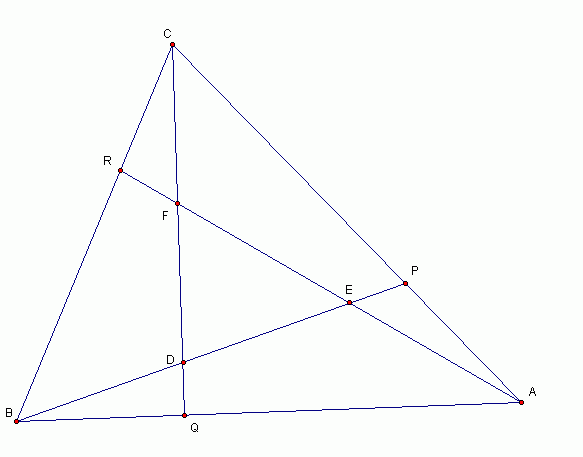
对于这一题，我的结论如下（写在这里，不然以后又忘了！！）
若
AP: PC = 1:λ
BQ: QA = 1:λ
CR: RB = 1:λ
（当然，这里我们可规定 λ≥0）
面积 FDE 和 面积 ABC  之比 ＝(1-λ)^2 /(λ^2 + λ + 1)

就是這一題



ABCD 是一个任意凸边四角形。
E 是 AC 与 BD 的交叉点。
证：面积 ADE 乘 面积 BCE = 面积 ABE 乘 面积 DCE

灰羊

pipi 于 15-10-2004 10:10 AM  说 :

对于这一题，我的结论如下（写在这里，不然以后又忘了！！）
若
AP: PC = 1:λ
BQ: QA = 1:λ
CR: RB = 1:λ
（当然，这里我们可规 ...

請教f(λ)=(1-λ)^2 /(λ^2 + λ + 1)
如何求得?

fritlizt

灰羊 于 7-11-2004 10:44 AM  说 :







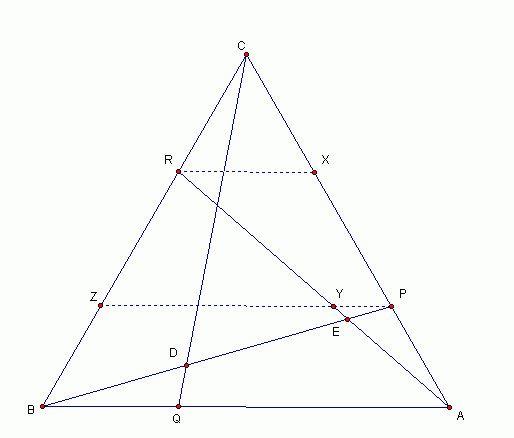
請教f(λ)=(1-λ)^2 /(λ^2 + λ + 1)
如何求得?

**cq 与 ra 的交叉点为F.

lets:
AP: PC = 1:λ
BQ: QA = 1:λ
CR: RB = 1:λ

RX : BA = 1: (1+λ)
RX : YP = 1: (λ)

所以 YP : BA = 1: (1+λ)(λ)

E 点对YP的距离为Z1, E 点对BA的距离为Z2
Z1 :Z2 = RX : YP = 1: (1+λ)(λ)

所以面积BEA : 面积BPA = (1+λ)(λ): [(1+λ)(λ)+1]
                      = (1+λ)(λ) :[λ^2+λ+1]

面积BPA : 面积ABC = 1 : [1+λ]

--> 面积BEA:面积ABC = (1+λ)(λ) :{[λ^2+λ+1][1+λ]}
                    = (λ) :[λ^2+λ+1]

--> 面积(BEA + AFC + CDB) : 面积ABC = 3λ :[λ^2+λ+1]

已知 面积(BEA + AFC + CDB + DEF) = 面积 (ABC)
所以 面积(DEF) : 面积 (ABC) = (λ^2+λ+1-3λ) :[λ^2+λ+1]
                            = (λ^2-2λ+1) :[λ^2+λ+1]
                            = (λ-1)^2 :[λ^2+λ+1]
                            =  (1-λ)^2 :[λ^2+λ+1]

[ Last edited by fritlizt on 9-11-2004 at 11:58 PM ]

pipi

不小心看到的几何问题，看似简单，不过。。。
试试吧！（求x）

pipi

若解了以上的题目，试试这个看来类似的。。。

也是求x。

~HeBe~_@

我只是找到四个equation....

Let the point which is two intersection line AE and BD be F

    angle CED = w
    angle DFE = x
    angle CDE = y
    angle CDB = z
   
w + x = 140
x - y = -20
y + z = 130
z - w = -30

不过好像是做不到。。。

不懂对不对。。。

整张纸被我涂鸦。。。

[ 本帖最后由 ~HeBe~_@ 于 18-8-2007 02:27 PM 编辑 ]

pipi

加油！只要你坚持，你可以找到的...
一张纸不够，在多几张吧！

[ 本帖最后由 pipi 于 18-8-2007 03:34 PM 编辑 ]

~HeBe~_@

可以再给一点提示吗？
要用什么方法呢？
因为若把以下的四个方程substitute的话，
是找不到答案哦。。

w + x = 140
x - y = -20  =〉x = -20 + y
y + z = 130  => y = 130 - z
z - w = -30  => z = -30 + w

Therefore,             w + x = 140
                w +(-20 + y) = 140
        w +(-20 + (130 - z)) = 140
w +(-20 + (130 - ((-30 + w)) = 140
                         140 = 140

根本找不到的哦。。

pipi

这就是它好玩的地方。。。
我是从以下网站看到的。。。（其实是先从一本数学杂志看到，再search google... ）
http://thinkzone.wlonk.com/MathFun/Triangle.htm
里头有hints,不过。。。看了别 :@ :@

原帖由 pipi 于 18-8-2007 08:42 AM 发表
不小心看到的几何问题，看似简单，不过。。。
试试吧！（求x）

x = 70 ?

原帖由 pipi 于 18-8-2007 08:45 AM 发表
若解了以上的题目，试试这个看来类似的。。。

也是求x。

x = 60 ?

pipi

原帖由 紫零星 于 19-8-2007 06:12 PM 发表


x = 70 ?



x = 60 ?

都不对。。。
不过能不能分享你的做法？
也许概念是对的，错在算法。。。