【纪念当年的帖子（2010）】Add Maths功课讨论区

数学神

回复  数学神


    答案不是7p吗？
长今 发表于 3-5-2010 23:56

可以show你的working吗？
我也有可能错的

vincent5081

版主有加分，怎么没有解决卡贴问题呢？
哎~

vincent5081

3P&4T  or  2P&5T  or  1P&6T

8C3x6C4 + 8C2x6C5 + 8C1x6C6 = 1016 ways
乙劍真人 发表于 4-5-2010 12:03 AM

真人，不用考虑到完全没有父母担任委员吗？
因为题目是不超过三位父母啊？
纯粹八卦一问。

乙劍真人

真人，不用考虑到完全没有父母担任委员吗？
因为题目是不超过三位父母啊？
纯粹八卦一问。
vincent5081 发表于 4-5-2010 08:34 PM

8C1x6C6..

如果 8C0，老师那边不可能 6C7 吧？

-------------------------------------------------------------------------
其实我也有遇到过类似的问题，
如果说要 form committee with 5 members
(condition = more teachers than parents)

i.e.: 6C3x8C2 + 6C4x8C1 + 6C5x8C0

我突然想不通那个 6C5x8C0 需要考虑吗？(很多书都说必须考虑)
但是我认为既然老师必须比父母多，0 父母也可以？

vincent5081

8C1x6C6..

如果 8C0，老师那边不可能 6C7 吧？

---------------------------------------------- ...
乙劍真人 发表于 4-5-2010 10:07 PM

不好意思，刚才太匆忙，没有看你的做法。
至于你的例子，既然是老师比父母多，0父母是可以接受的。
1比0多，哈哈哈~

乙劍真人

不好意思，刚才太匆忙，没有看你的做法。
至于你的例子，既然是老师比父母多，0父母是可以接受的。
1比 ...
vincent5081 发表于 4-5-2010 10:27 PM

哦..好的..
刚开始我以为 0 不能做比较嘛..

谢谢您..

永遠愛著許瑋倫

最近温习回function..遇到问题,请指教
1）Sketch the graph of
a.f:x->|3x-8| for 0 -< x -< 4
b.g:x-> -|2x-1| for 0-< x -<3

-< 是 equal or lower than..因为不会打那个符号

乙劍真人

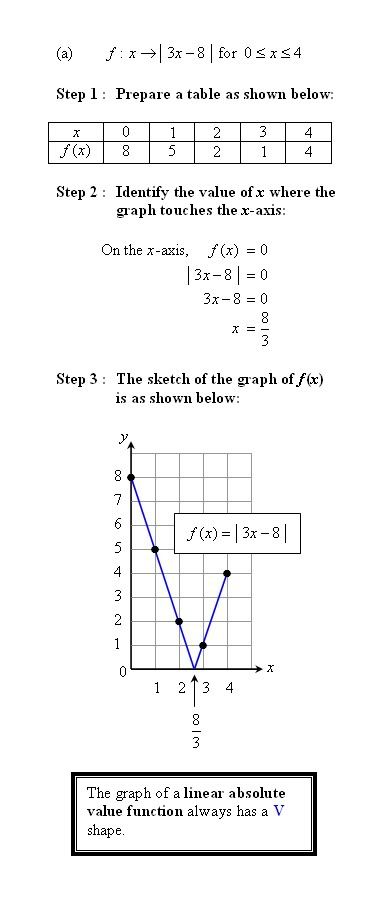
最近温习回function..遇到问题,请指教
1）Sketch the graph of
a.f:x->|3x-8| for 0 -< x -< 4
b.g:x-> -|2x-1| for 0-< x -<3

-< 是 equal or lower than..因为不会打那个符号
永遠愛著許瑋倫 发表于 12-5-2010 04:38 PM

我做 a 给你看，b 的你自己试试..

改次遇到这个 pattern 的题目参考我的方法就行了..加油..^^

永遠愛著許瑋倫

真人老師，你可不可以畫(b)的，我想看看對不對...感覺怪怪的

乙劍真人

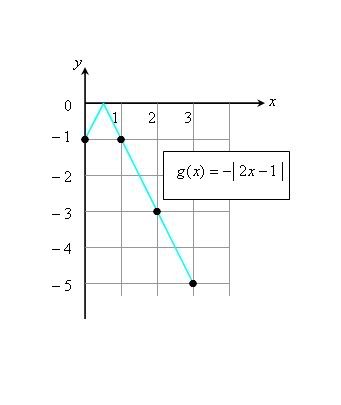
真人老師，你可不可以畫(b)的，我想看看對不對...感覺怪怪的
永遠愛著許瑋倫 发表于 12-5-2010 11:30 PM

你应该画对啦，有 -ve 的 absolute value function，graph 是倒转 V 的：

永遠愛著許瑋倫

我想問問些基本問題
g(x)=-|2(2)-1|
=-|3|
=-(-3)  or  -(3)
=3        or    -3
對不對啊？
如果對，為什麼那題要用-3放在 y-axis
還有,如果問題加個Hence,determine the range of function...該怎麼回答(a)和(b)

dollyeye

Prove the following identities:
(a) cos(A+B)/cos A cos B = 1- tan A tan B
(b)sin(A+B)/cos A cos B = tan A + tan B

怎样做哦？？

乙劍真人

我想問問些基本問題
g(x)=-|2(2)-1|
=-|3|
=-(-3)  or  -(3)
=3        or    -3
對不對啊？
如果對，為什麼那題要用-3放在 y-axis
還有,如果問題加個Hence,determine the range of function...該怎麼回答(a)和(b)
永遠愛著許瑋倫 发表于 13-5-2010 02:56 PM

不对，只有当 function modulus 的时候才能放 +/-；

e.g: / x+1 / = 2
(x+1) = 2        or -(x+1) = 2
      x = 2 - 1              x = -2 - 1
        = 1                   x = -3

也就是说当 x = 1 or x = -3 会造成那个 function = 2 咯..

回题目：
/3/ = 3，不必弄 -3 了。

range of function 就是看 y-axis 的范围：
（a）0 <= f(x) <= 8
（b）-5 <= g(x) <= 0

乙劍真人

Prove the following identities:
(a) cos(A+B)/cos A cos B = 1- tan A tan B
(b)sin(A+B)/cos A cos B = tan A + tan B
dollyeye 发表于 13-5-2010 07:55 PM

用 compound-angle formulae 破解：

(a) LHS = (cosAcosB - sinAsinB) / cosAcosB
           = cosAcosB/cosAcosB - sinAsinB/cosAcosB
           = 1 - tanAtanB
           = RHS (Proven)

(b) LHS = (sinAcosB + cosAsinB) / cosAcosB
           = sinAcosB/cosAcosB + cosAsinB/cosAcosB
           = sinA/cosA + sinB/cosB
           = tanA + tanB
           = RHS (Proven)

永遠愛著許瑋倫

真人老師，有3題需要指教我也覺得不好意思了
1)If the points A(0,8),B(8,0) and C(x,y) lie on the circumference of a circle with diameter AB,find the equation of the locus of the moving point C.

2)Given the points P(0,1) and Q(6,4),find the equation of the locus of a moving point C such that the triangle PCQ always has a right angle at C.

3)A point Q moves along the circumference of a circle with centre P(3,2).The circumference passes through the points A(0,-2) and B(m,5)
a.Find
  i.the equation of the locus of the point Q
  ii.the values of m

b.The tangent to the circle at point A intersects the x-axis at point T.Find the area of OAT

乙劍真人

真人老師，有兩題需要指教
1)If the points A(0,8),B(8,0) and C(x,y) lie on the circumference of acircle with diameter AB,find the equation of the locus of the movingpoint C.

2)Given the points P(0,1) and Q(6,4),find the equation of the locus ofa moving point C such that the triangle PCQ always has a right angle atC.

(1) 关键：ACB 一定是 90 度..
therefore M_AC x M_BC = -1
[(y-8)/(x-0)] x [(y-0)/(x-8)] = -1
             [y(y-8)] / [x(x-8)] = -1
                          y^2 - 8y = -x^2 + 8x

i.e. equation of the locus of the point C is x^2 + y^2 - 8x - 8y = 0.

(2) 关键：PCQ = 90 度
therefore M_PC x M_QC = -1
[(y-1)/(x-0)] x [(y-4)/(x-6)] = -1
                        (y-1)(y-8) = -1(x)(x-6)
                    y^2 - 5y + 4 = -x^2 + 6x

i.e. equation of the locus of the point C is x^2 + y^2 - 6x - 5y + 4 = 0.

乙劍真人

真人老師，有3題需要指教我也覺得不好意思了
3)A point Q moves along thecircumference of a circle with centreP(3,2).The circumference passesthrough the points A(0,-2) and B(m,5)
a.Find
  i.the equation of the locus of the point Q
  ii.the values of m

b.The tangent to the circle at point A intersects the x-axis at point T.Find the area of OAT

(a)(i) Distance PA = sr (0-3)^2 + (-2-2)^2
                          = sr (9+16)
                          = sr 25
                          = 5 unit

Let Q = (x,y)                           PQ = PA
                    sr (x-3)^2 + (y-2)^2 = 5
       x^2 - 6x + 9 + (y^2 - 4y + 4) = 25

i.e. the equation of the locus of point Q = x^2 + y^2 - 6x - 4y - 21 = 0 (*)

(a)(ii) sub B(m,5) into equation (*)
              x^2 + y^2 - 6x - 4y - 21 = 0
       m^2 + (5)^2 - 6m - 4(5) - 21 = 0
                            m^2 - 6m - 16 = 0
                                (m+2)(m-8) = 0
                                              m = -2 or m = 8

(b) Area OAT
先找 equation of AT:

M_PA = (2+2)/(3-0)
      = 4/3
M_AT = -3/4

Equation of AT,   y - (-2) = -3/4 (x - 0)
                           y + 2 = -3/4 x
                         4y + 8 = -3x
At T, let y = 0,  4(0) + 8 = -3x
                                 x = 8/-3

therefore T = (-8/3, 0)

i.e. O(0,0), A(0,-2) & T(-8/3, 0)
Area OAT = formulae AREA
              = 8/3 units^2

永遠愛著許瑋倫

卡了兩天了。。。真厲害

乙劍真人

卡了兩天了。。。真厲害
永遠愛著許瑋倫 发表于 15-5-2010 12:15 PM

那你有看到我的解答没？

永遠愛著許瑋倫

卡了3天野...還沒修復？？？