STPM-学校功课討論区

~HeBe~_@

-3x^2 / (x^3 + 1)^2

chwk87

原帖由 ~HeBe~_@ 于 17-11-2007 12:29 PM 发表
-3x^2 / (x^3 + 1)^2

对不起。应该是怎样kamir才是。写错了。

~Lucifer~

答案是这个吗？1/(1+x^3)拆成(1/3)/(x+1)-(1/3)(x-2)/(x^2-x+1),然后分两个部份来做，我拿到(1/3)ln(x+1)-(1/6)ln(x^2-x+1)-(1/√3)[(tan-1)(2x-1)/(√3)].tan-1是anti tan.不大肯定 ，请大家指教。

[ 本帖最后由 ~Lucifer~ 于 17-11-2007 04:59 PM 编辑 ]

chwk87

请问你们可以也把算草写出来吗？对不起，现在我还没有答案。

dunwan2tellu

原帖由 ~Lucifer~ 于 17-11-2007 04:58 PM 发表
答案是这个吗？1/(1+x^3)拆成(1/3)/(x+1)-(1/3)(x-2)/(x^2-x+1),然后分两个部份来做，我拿到(1/3)ln(x+1)-(1/6)ln(x^2-x+1)-(1/√3)[(tan-1)(2x-1)/(√3)].tan-1是anti tan.不大肯定 ，请大家指教。

Lucifer 的答案应该是   + (1/sqrt[3])ArcTan[(2x-1)/sqrt[3]]

partial fraction

1/(x^3+1) = 1/3 * ( 1/(x+1) - (x-2)/(x^2-x+1))
          = 1/3 * (1/(x+1) - 1/2 * (2x-4)/(x^2 - x + 1) )
          = 1/3 * (1/(x+1)) - 1/6 * ( (2x-1)/(x^2 - x + 1) - 3/(x^2 - x + 1))

1/(x+1) integrate => ln(x+1)

(2x-1)/(x^2-x+1) integrate => ln(x^2-x+1)

1/(x^2-x+1) integrate => 2sqrt[3] * ArcTan[(2x-1)/sqrt[3]]

chwk87

原帖由 dunwan2tellu 于 18-11-2007 01:09 PM 发表


Lucifer 的答案应该是   + (1/sqrt[3])ArcTan[(2x-1)/sqrt[3]]

partial fraction

1/(x^3+1) = 1/3 * ( 1/(x+1) - (x-2)/(x^2-x+1))
          = 1/3 * (1/(x+1) - 1/2 * (2x-4)/(x^2 - x + 1) ) ...

谢谢。明白了。

Leong13

請幫忙solve
show that the centres of the circles passing through the points (3,2) and ( 6,3) are located on the line 3x + y = 16. two of these circles touch the line x+2y=2. find the equations of both these circles. determine the point on the line x +2y=2.

Leong13

還有一題
given three points A (3,3), B(-1,5), C(6,0) and a straight line L with equation y= mx-8m-6.If L intersects triangle ABC, find the range of m.

~Lucifer~

L intersects triangle ABC的意思是？我了解能力不大好...

dunwan2tellu

原帖由 Leong13 于 18-11-2007 06:50 PM 发表
還有一題
given three points A (3,3), B(-1,5), C(6,0) and a straight line L with equation y= mx-8m-6.If L intersects triangle ABC, find the range of m.

如果 M(AB) 表示 gradient of AB ， 那么

M(AB) = -1/2
M(AC) = -1
M(BC) = -5/7

y = m(x-8) - 6 经过一个 fix point , (8,-6)

设 这个点是 P = (8,-6) ，那么

M(AP) = -9/5
M(BP) = -11/9
M(CP) = -3

做图不难发现要他们 intersect 的话，就必须有

M(CP) =< m =< M(BP)


-3 =< m =< -11/9

請幫忙solve
show that the centres of the circles passing through the points (3,2) and ( 6,3) are located on the line 3x + y = 16. two of these circles touch the line x+2y=2. find the equations of both these circles. determine the point on the line x +2y=2.

如果你还记得如何利用圆形 circumference 上的 2 个点来找出他的 center 的话，你就知道如何证明 3x+y=16 (提示：perpendicular bisector line of the two point)

要找 equation 的话，设 center = (a,b)

3a + b = 16 .....(i)  center pass tru 3x+y=16

(3-a)^2 + (2-b)^2 = (a+2b-2)^2/5 ....(ii)  radius from center to (3,2) = radius from center to tangent line

solve (i),(ii) 就可以得到两个 (a,b)

[ 本帖最后由 dunwan2tellu 于 19-11-2007 05:54 PM 编辑 ]

Leong13

可是我們怎樣知道她是perpendicular bisector line of the two point

Leong13

我還有問題
1. Find the ratio of the term in a^r to the term in a^r+1 in the expansion of (a+b)^n.

2.(1-3x^2)^-n, modulus x <1/2, find the sixth term

dunwan2tellu

原帖由 Leong13 于 19-11-2007 10:31 PM 发表
可是我們怎樣知道她是perpendicular bisector line of the two point

回忆以前 form 2 circle 的 topic . 给你一个圆形，要你找他的 center 的话，你是不是先画一条 chord , 然后把它分一半。然后又找另一个 chord 和分一半。两条线的交叉点就是 center . 用这道理就可以知道为什么 center 是在 perpendicular bisector line 上面。

另一个方法也可以得到 3x+y=16

设 center = (x,y) 那么 center 到 那两个 point 的 distance 是同样的，所以你就可以用 distance formula 来 form equation .

i.e (3-x)^2 + (2-y)^2 = (6-x)^2 + (3-y)^2

...
...

原帖由 Leong13 于 19-11-2007 10:34 PM 发表
我還有問題
1. Find the ratio of the term in a^r to the term in a^r+1 in the expansion of (a+b)^n.

2.(1-3x^2)^-n, modulus x <1/2, find the sixth term

1 . r th term : A = nCr * a^r * b^(n-r) . 我 assume 这里 n 是 positive integer .

    (r+1) th term : B = nC(r+1) * a^(r+1) * b^(n-r-1)

A/B = [nCr * a^r * b^(n-r)]/[nC(r+1) * a^(r+1) * b^(n-r-1) ]
    = nCr/nC(r+1) * b/a
    = n!/(r!(n-r)!) * (r+1)!(n-r-1)!/n! * b/a
    = (r+1)/(n-r) * b/a

2. （1 - 3x^2)^-n = 1 + n * 3x^2 + (-n)(-n-1)/2! * (-3x^2)^2 + ...

6th term : (-n)(-n-1)(-n-2)(-n-3)(-n-4)(-n-5)/6! * (-3x^2)^6 = .....

[ 本帖最后由 dunwan2tellu 于 19-11-2007 11:14 PM 编辑 ]

zfc

有个关于probability的问题要请教：
A lady attends interviews at 3 companies X, Y and Z. Based on her own judgement, she believes that the probability that she will be offered a post at the companies are 2/5 at X, 3/10 at Y and 1/10 at Z. What is the probability that the lady gets a job at any one of the 3 companies?
答案是57/125。请问怎样获得这个答案呢？

hamilan911

P(gets 1 job) = P(拿到X，拿不到Y和Z) + P(拿到Y，拿不到X和Z) + P(拿到Z，拿不到X和Y)

zfc

哦，谢谢。之前原来我按错计算机了。

zfc

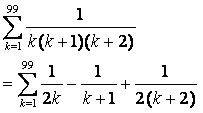
请问怎样做到答案等于5049/20200？

[ 本帖最后由 zfc 于 1-2-2008 10:46 PM 编辑 ]

kenny56

1/k(k+1)(k+2)
=1/(k+!)*1/k*1/(k+2)
=1/2*1/(k+1)(1/k-1/(k+2))
=1/2(1/k(k+1))-1/(k+1)(k+2))

E for summation

E1/2(1/k(k+1))-1/(k+1)(k+2))
=1/2(1/2-1/6+1/6-...............-1/10100)
=1/2(1/2-1/10100)
=5049/20200

dunwan2tellu

或考虑

1/2 * (1/k - 1/(k+1))  - 1/2 * (1/(k+1) - 1/(k+2))

两个 summation

zfc

谢谢两位高手！