几何问题

fritlizt

pipi 于 30-7-2004 10:50 AM  说 :
我又想到一题几何题：

如上图，点P 与 点Q 分别在AB 与AD 上，使到
三角形 APQ 的周长 是 正方形 ABCD 的周长 的一半。
试证：
( ...

我把

转成


已知 APQ周长等于 ABCD周长 的一半。
PQ = PB+QD = PQ'

PQ = PQ' , QC = Q'C
所以 PC 是 角QCQ' 平分线。
角QCQ' = 角DCB = 90

QCP = 90/2 = 45度。

[ Last edited by fritlizt on 21-8-2004 at 05:44 PM ]

pipi

fritlizt 于 21-8-2004 05:43 PM  说 :
已知 APQ周长等于 ABCD周长 的一半。
PQ = PB+QD = PQ'
PQ = PQ' , QC = Q'C
所以 PC 是 角QCQ' 平分线。
角QCQ' = 角DCB = 90
QCP = 90/2 = 45度。

为什么PQ = PB+QD = PQ'
（我们只有PQ+QA+AP=1/2 (AB+BC+CD+DA)而已啊！）

fritlizt

pipi 于 21-8-2004 09:36 PM  说 :

为什么PQ = PB+QD = PQ'
（我们只有PQ+QA+AP=1/2 (AB+BC+CD+DA)而已啊！）

PQ+QA+AP=1/2 (AB+BC+CD+DA)
        = AB + AD
        = BP + PA +AQ + QD

所以PQ = PB + QD

我再把三角形 QCD 搬上去，变成三角形 BCQ ,
QD = BQ'
PQ = PB + QD
   = PB + BQ'
   = PQ'

[ Last edited by fritlizt on 22-8-2004 at 01:12 AM ]

pipi

fritlizt 于 22-8-2004 01:02 AM  说 :
PQ+QA+AP=1/2 (AB+BC+CD+DA)
        = AB + AD
        = BP + PA +AQ + QD
所以PQ = PB + QD
我再把三角形 QCD 搬上去，变成三角形 BCQ ,
QD = BQ'
PQ = PB + QD
   = PB + BQ'
   = PQ'

刚才发完贴后发现自己错了！！
你的确实是很不错的解法！！好！！
过几天，我贴上我的做法，是用代数的方法的。

fritlizt

来多一题吧。


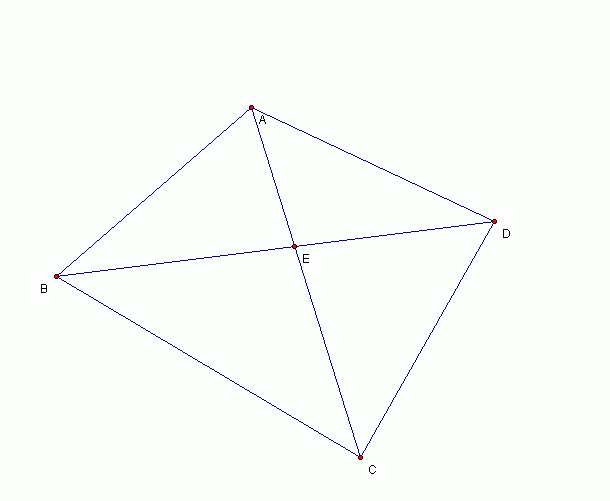
ABCD 是一个任意凸边四角形。
E 是 AC 与 BD 的交叉点。
证：

面积 ADE 乘 面积 BCE = 面积 ABE 乘 面积 DCE


p/s : 怎么好像没有人来解几何问题的？？？？

pipi

fritlizt 于 22-8-2004 05:24 PM  说 :
p/s : 怎么好像没有人来解几何问题的？？？？  

fritlizt网友，我支持你！！
（虽然你的第一题我仍然解不到。。。）
你刚刚贴的这一题，我有些头绪了。。。
看明天能不能给你答案！！

pipi

ABCD 是一个任意凸边四角形。
E 是 AC 与 BD 的交叉点。
证：面积 ADE 乘 面积 BCE = 面积 ABE 乘 面积 DCE

这个不难！
设角 AEB=α。
所以角CED＝α，角AED＝π－α＝角CEB。
我们有 sin(AEB)=sin(CED)=sin(AED)=sin(CEB)=sinα。
面积 ADE  = (1/2)(AE)(DE)(sinα)
面积 BCE  = (1/2)(BE)(CE)(sinα)
面积 ABE  = (1/2)(AE)(BE)(sinα)
面积 DCE  = (1/2)(DE)(CE)(sinα)
由之得证！


（一个小插曲：刚刚跑步时发现我给自己骗了
一直以为是
面积 ADE 加 面积 BCE = 面积 ABE 加 面积 DCE。。。 ）

fritlizt

pipi 于 22-8-2004 07:28 PM  说 :

这个不难！
设角 AEB=α。
所以角CED＝α，角AED＝π－α＝角CEB。
我们有 sin(AEB)=sin(CED)=sin(AED)=sin(CEB)=sinα。
面积 ADE  = (1/2)(AE)(DE)(sinα)
面积 BCE  = (1/2)(BE)(CE)(sinα)
面积 ABE  ...

阿哈，对了。 这样快就给到我答案了。
我有另一个解法，迟些post上来。
不过相比之下，你的比较简单。
下次要找难度较高的了。

fritlizt

1)


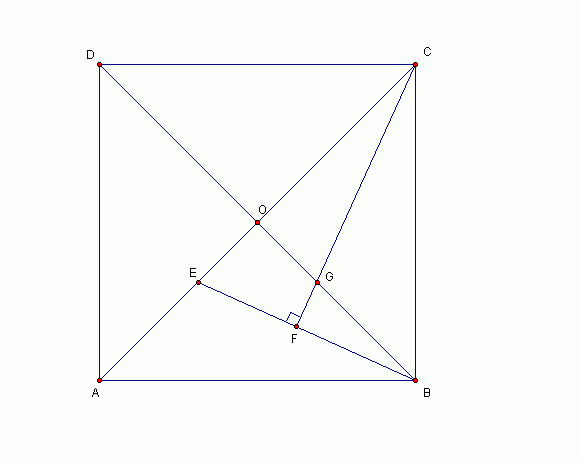
已知正方形ABCD 的对角线 AC, BD 交于点 O, E 是 AO 上的一点， CF 垂直 BE 于点 F, 交 BO 于点 G.
求证： OE = OG

2)


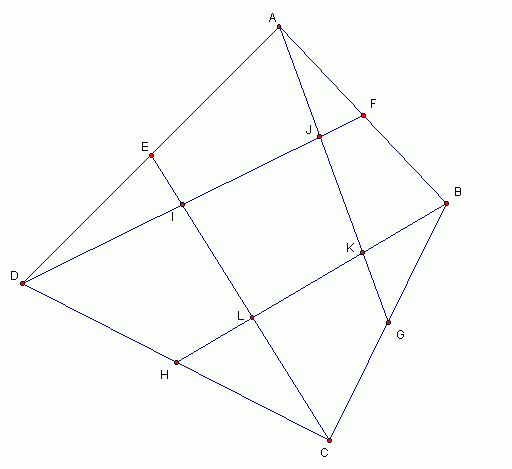
ABCD 是一个任意凸边四角形。  EFGH 分别是四个边的中心点。
求证：面积AJF +面积BKG + 面积CLH +面积DIE = 面积IJKL

p/s: 假期到了，先贴上两题，希望能tahan到三个星期。三个星期内我应该不会进cari 论坛。

[ Last edited by fritlizt on 25-8-2004 at 03:18 AM ]

pipi

fritlizt 于 25-8-2004 02:58 AM  说 :
1)


已知正方形ABCD 的对角线 AC, BD 交于点 O, E 是 AO 上的一点， CF 垂直 BE 于点 F, 交 BO 于点 G.
求证： OE = OG

先解了这一题！
要证明 OE = OG 只需证明 三角形 OEB 全等于 三角形 OGC 即可！

设 ∠EBA ＝α  。
由三角形 AEB，
外角∠OEB ＝∠EAB ＋ ∠EBA  
          ＝45度 + α 。
因为 ∠EBA ＝α ，所以 ∠FBG = 45度 - α ，
也就是说  ∠OGC = ∠FGB = 45度 ＋ α         (90度 - ∠FBG)
所以 ∠OEB ＝ ∠OGC。
留意 OB ＝ OC 及 ∠EOB ＝ ∠GOC。
所以 三角形 OEB 全等于 三角形 OGC，即 OE = OG。
完毕！！

[ Last edited by pipi on 27-8-2004 at 12:06 PM ]

pipi

fritlizt 于 25-8-2004 02:58 AM  说 :
2)


ABCD 是一个任意凸边四角形。  EFGH 分别是四个边的中心点。
求证：面积AJF +面积BKG + 面积CLH +面积DIE = 面积IJKL

这一题之前解过了。。。

Crissaegrim

fritlizt 于 25-8-2004 02:58 AM  说 :
1)


已知正方形ABCD 的对角线 AC, BD 交于点 O, E 是 AO 上的一点， CF 垂直 BE 于点 F, 交 BO 于点 G.
求证： OE = OG

对角，所以角FGB＝角OGC，角COG＝角BFG＝９０度，
因此角OCG＝角FBG。
正方形ABCD，对角线BO＝CO，内角平分成角EOB＝角COG＝９０度，
由此可得三角形COG＝三角形BOE，OG＝OE。

酱说会不会较简单？我觉得我的方法好象有些漏洞，可以指点一下吗？

Crissaegrim:

Crissaegrim 于 28-8-2004 06:17 PM  说 :

对角，所以角FGB＝角OGC，角COG＝角BFG＝９０度，
因此角OCG＝角FBG。
...

应该对了！！
很好的解答，加油！！(共勉之)

fritlizt

pipi 于 26-8-2004 10:56 PM  说 :

这一题之前解过了。。。

之前解了吗？没看到eh......

fritlizt

pipi 于 30-7-2004 02:21 PM  说 :
再来一题几何题：

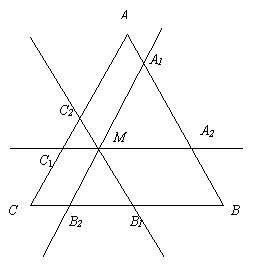
如上图，点 M 是 任意三角形 ABC 里的任意一点。
过 点 M ， 画三条分别与 AB，BC 及 CA 平行的线。

S 代表面 ...

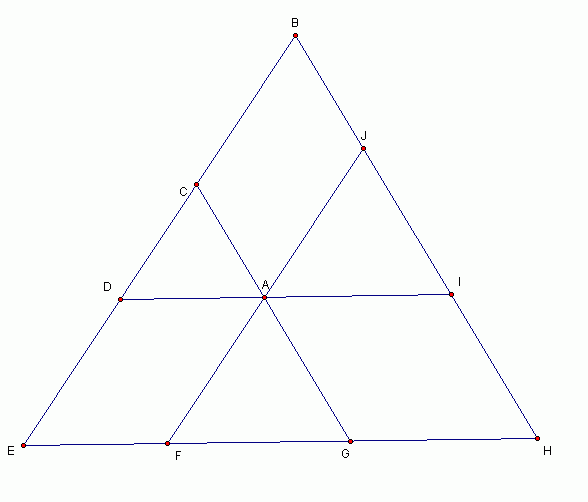
角CAJ = 角CAJ = 角FAG =  x
角CAD = 角IAG = 角IHG = y
角JAI = 角DAF = 角DEF = z

BJAC 的面积为 JA.AC.sin(x)
IAGH 的面积为 AG.IA.sin(y)
DAFE 的面积为 DA.AF.sin(z)

FAG 的面积为 1/2.AF.FG.sin(x)
CAD 的面积为 1/2.CA.AD.sin(y)
JAI 的面积为 1/2.JA.AI.sin(z)

BJAC.AIGH.DAFE = JA.AC.AG.IA.DA.AF.sin(x).sin(y).sin(z)
FAG.CAD.JAI = 1/8.JA.AC.AG.IA.DA.AF.sin(x).sin(y).sin(z)

(BJAC.AIGH.DAFE)/(FAG.CAD.JAI) = 8

fritlizt

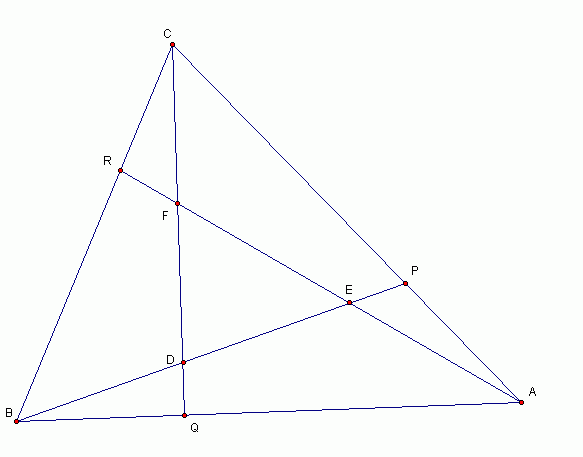
ABC 是一个任意三角形。

AP:AC = 1:3
BQ:BA = 1:3
CR:CB = 1:3

求 ：面积 FDE 占了 总面积 ABC  得几分之几。

pipi

这几天，蛮忙的。。。
不要紧，等我今晚在梦中做（楼上的问题。。。）！！！

pipi

哈，昨晚倒没有在梦中做这题。。。
不过，醒来时有个想法：
若题目改成
AP: PC = 1:λ
BQ: QA = 1:λ
CR: RB = 1:λ
（当然，这里我们可规定 λ≥0）
问：面积 FDE 和 面积 ABC  之比  会不会是一个只是 depend on λ 的函数呢？
若是，我们可将该函数设为 f(λ)。
那么，进一步想，f(λ) 应该满足以下几点：
(i)   0 ≤ f(λ) ≤ 1 for all λ≥0
(ii)  f(λ) = f(1/λ)
(iii) 当 λ 趋近于 0+ 时， f(λ)=1
(iv)  f(1)=f'(1)=0, 也就是说：f(λ)＝(λ-1)^2 g(λ) for some g

当然，以上只是猜想，并未得到任何证明。。。
若有新的进展，再来分享！！
各位，也来玩玩吧！！

[ Last edited by pipi on 25-9-2004 at 10:02 AM ]

fritlizt

你的猜想是没错的。虽然我还没一个proper的证明。我只是把 λ 换成其他的value, 发觉面积 FDE 和 面积 ABC  之比  会是一个只是 depend on λ 的函数。



而且想过后，这几点也没错。
(i)   0 ≤ f(λ) ≤ 1 for all λ≥0
(ii)  f(λ) = f(1/λ)
(iii) 当 λ 趋近于 0+ 时， f(λ)=1

只是
(iv)  f(1)=f'(1)=0, 也就是说：f(λ)＝(λ-1)^2 g(λ) for some g
这点我还没确定。

不要紧，解了这个题目后， 我们可以在进一步证明面积 FDE 和 面积 ABC  之比  会是 depend on λ 的函数。

pipi

之前讨论的那一题，我猜我得到了它一般性的答案吧！！
即找到了 f(λ)。
暂时先不公布答案，让大家再试试。
至于原题的答案（当 λ＝2），是 1/7 吧！！
（如果这答案不对，那我那一般性的答案也就错了！！）