University-数学讨论区-Calculus, Real Analysis

~HeBe~_@

Calculus
Calculus, Multi-Variable Calculus....

看到你们也这样开了STPM，SPM的数学讨论区

希望有任何难题可以在此帖讨论哦！


[ 本帖最后由 ~HeBe~_@ 于 27-5-2008 11:50 PM 编辑 ]

pipi

我来凑一脚，这是老题目了，再次拿来炒一炒，热一热。


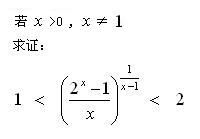
        （ 提示：利用 Mean Value Theorem ）

pipi

再来一题（某大学的考试题目）：
（为了方便，请容许我以英文书写）
Let f be a twice differentiable function defined on R satisfying f(0)=0, f'(0)=1 and f"(x) > 0 for all x in R. Define h(x)=f(x)/x , if x not equal to 0 and h(x) = 1 if x=0.

(i) Prove that for any x>0, there exists a number c in (0,x) such that

h'(x) = [f'(x) - f'(c)]/x

(ii) Show that h is increasing on R.

dunwan2tellu

原帖由 pipi 于 29-4-2007 10:15 AM 发表
再来一题（某大学的考试题目）：
（为了方便，请容许我以英文书写）
Let f be a twice differentiable function defined on R satisfying f(0)=0, f'(0)=1 and f"(x) > 0 for all x in R. Define h(x ...

h'(x) = [f'(x) - f(x)/x]/x

from MVT , there exist a c in (0,x) such that [f(x)-f(0)]/(x-0) = f'(c) <==> f'(c) = f(x)/x

hence h'(x) = [f'(x)-f'(c)]/x

Since f''(x) > 0 and f'(0) = 1 , we know that f'(x) is increasing ,i.e f'(x) > f'(y) for all x > y

hence f'(x) > f'(c) ==> h'(x) > 0

we conclude that h(x) is increasing on R

~HeBe~_@

1)State Green Theorem
2)State Stokes Theorem
3)State Divergence Theorem

~HeBe~_@

这么美的theorem没人去state吗？

yaahoo

我相信这里的许多访客,包括我;还搞不清楚那是什么跟什么呢!!!

能不能跟我们分享一下你为何觉得它们优美呢？ 顺便叙述一下好吗?

~Lucifer~

大家好...请问有人可以为我大概讲解下Stokes Theorem和Divergence Theorem吗？我这个sem的field theory有读到，可是我只会apply formula吧了，有人可以讲解它们的奥妙的地方吗？谢谢！

~HeBe~_@

你是在这个sem拿Advance Calculus 吗？

~Lucifer~

我读engineering的,这个sem拿field theory,有介绍这两个theorem,不过并不深入，你可以为我详细解说吗？

~HeBe~_@

我对这两个theorem也不是深。。只是我的讲师说他是个很美的theorem罢了。。。
若state theorem因该还可以吧。。。
若要更深入就不行咯。。
我是读Applied Maths de...在Advance Calculus认识到它们。。。

yaahoo

如果你看了该定理，仍旧看不到其优美的地方；不妨阅读以下的连接

http://www.math.sinica.edu.tw/math_media/d214/21403.pdf


看看数学家如何评价该定理及了解其物理意义，相信读工程的同道会比我们念纯数的了解更透彻。

我们可以针对文中所提到的内容再讨论，这样可能会更有效率一些。

感觉上文中所提的边界和mathlim所问的体积，周长和表面积好象有微妙的关系。

[ 本帖最后由 yaahoo 于 18-9-2007 09:28 AM 编辑 ]

~HeBe~_@

1)State Green Theorem


2)State Stokes Theorem


3)State Divergence Theorem

chan1314

原帖由 ~Lucifer~ 于 18-9-2007 12:28 AM 发表
我读engineering的,这个sem拿field theory,有介绍这两个theorem,不过并不深入，你可以为我详细解说吗？

我明天就考这颗啊。。。。
很美的theory , 也干掉不少人。。。

比如说

Q= integrate p dv,
int J.ds = d/dt (int p dv)
int div J.dv = int par P/par t dv
int (div.J + par p/ par t ) dv =0
div.J + par p/ par t  = 0

把closed surface integral 换成 volume integral.

stoke 就把 closed path line integral 换成 surface integral 。

当这个加上 coordinate system , 就 double kill 了。

chan1314

请问您是不是 utar de applied math wif comp ?

yaahoo

一个了解这些定理最基本的步骤应该就是要知道积分符号下的函数所代表的意义了。如 curl F 和 div F 到底是什么东东？这些东东的含义又是什么？dot 上 dS 后又代表什么？左边亦然。那定理就很形象化了。

有些东西自己体会比听他人说来得有成就感，所以暂时 dunwan2tellu

[ 本帖最后由 yaahoo 于 18-9-2007 11:16 AM 编辑 ]

~HeBe~_@

哈哈！果然是 "double kill"哦。。。
我还以为是在玩游戏。。
幸亏没有triple kill。。。。

chan1314

原帖由 ~HeBe~_@ 于 18-9-2007 11:16 AM 发表

哈哈！果然是 "double kill"哦。。。
我还以为是在玩游戏。。
幸亏没有triple kill。。。。

差不多咯。
预计明天的考试全班fail .

还好有 uniqueness theorem , 不然真的god like 了。。。。

~HeBe~_@

哈哈！我们只是学到皮毛而已。。。

~HeBe~_@

那我们就要等dunwan2tellu回来才请教他咯。。。
不过，别人的考试就不能等咯。。。