|
|
有个问题我做了很久还是得不到他的答案。
所以开个新贴,大家来帮个忙,看看能不能解决这个问题。

给任何凸边四角形,证:6> ABCD/IJKL >= 5.
已知 AJF + BKG + CLH + DIE = IJKL。
E,F,G,H 分别是四个边的中心点。
我的翻译水准不好。我把英文的问题也写出来。
For any convex quadrilateral, prove: ABCD/IJKL is always greater than or equal to 5 and less and 6 where AJF + BKG + CLH + DIE = IJKL and E,F,G,H are the midpoint for each segment.
[ Last edited by fritlizt on 22-7-2004 at 10:16 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 12:48 PM
|
显示全部楼层
发表于 23-7-2004 12:48 PM
|
显示全部楼层
fritlizt 于 22-7-2004 09:30 PM 说 :
给任何凸边四角形,证:6> ABCD/IJKL >= 5.
已知 AJF + BKG + CLH + DIE = IJKL。
E,F,G,H 分别是四个边的中心点。
For any convex quadrilateral, prove: ABCD/IJKL is always greater than or equal to 5 and less and 6 where AJF + BKG + CLH + DIE = IJKL and E,F,G,H are the midpoint for each segment.
ABCD 意思是 ABCD 的面积吗?? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-7-2004 12:51 PM
|
显示全部楼层
|
对,ABCD AJF BKG CLH DIE IJKL 指的都是他们的面积。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 01:02 PM
|
显示全部楼层
发表于 23-7-2004 01:02 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 01:27 PM
|
显示全部楼层
发表于 23-7-2004 01:27 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-7-2004 01:43 PM
|
显示全部楼层
我之前也有这个想法。不过经过电脑的一些运算过后,发现 IJ/JF, JK/KG, KL/LH, LI/IE 里,必有两个ratio 大过二,两个ratio 小过二。 如果四个ratio 都等于二, 那ABCD/IJKL 就等于五了。
所以 2< IJ/JF, JK/KG, KL/LH, LI/IE < 3 不成立。

还有,再加以补充一下, 本来的问题是ABCD/IJKL >= 5, 只是我无论用电怎么算也好,都没有一个情况下ABCD/IJKL >=6 ,除非ABCD形成一个三角形。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-7-2004 01:54 PM
|
显示全部楼层
请考虑以下情况:
ABCD 为边长 2 的正方形。那么它将满足
AJF + BKG + CLH + DIE = IJKL (如你题目的。。。它们也代表面积)
mmm......我检查了题目。题目没错。还有,
AJF + BKG + CLH + DIE = IJKL 并不再只有ABCD 是正方形的情况之下才成立。
以被证,给任何凸边四角形(convex quadrilateral) AJF + BKG + CLH + DIE = IJKL 。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 02:07 PM
|
显示全部楼层
发表于 23-7-2004 02:07 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-7-2004 02:56 PM
|
显示全部楼层
"AJF = BKG = CLH = DIE = 1/2 * 1/2 * sqrt(3)/2""
对不起,小弟不是很明白你是如何得到这个式子。
可以解释一下吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 03:10 PM
|
显示全部楼层
发表于 23-7-2004 03:10 PM
|
显示全部楼层
我们有 AF = 1
∠JAF = ∠BAG = pi/6
所以 AJ = cos(pi/6) = sqrt(3)/2
∠JFA = ∠BGA = pi/3
所以 JF = cos(pi/3) = 1/2
所以 AFJ = 1/2 * 1/2 * sqrt(3)/2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 05:50 PM
|
显示全部楼层
发表于 23-7-2004 05:50 PM
|
显示全部楼层
pipi 于 23-7-2004 03:10 PM 说 :
我们有 AF = 1
∠JAF = ∠BAG = pi/6
所以 AJ = cos(pi/6) = sqrt(3)/2
∠JFA = ∠BGA = pi/3
所以 JF = cos(pi/3) = 1/2
所以 AFJ = 1/2 * 1/2 * sqrt(3)/2
用回边长2的正方形:
角JAF好像不是PI/6...
角JFA也好像不是PI/3...
我算到tan(角JAF)是0.5
所以我算到AJ = 2/sqrt(5), JF = 1/sqrt(5)
所以JAF的面积是1/5.
因为有四个,所以是4/5。所以IJKL的面积是4/5。
所以ABCD/IJKL = 4/(4/5) = 5 (刚刚好)
(这是用边长2的正方形来验证,真正证明还不会做。。)
不知对吗?
[ Last edited by jwyong on 23-7-2004 at 05:54 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-7-2004 07:04 PM
|
显示全部楼层
jwyong 于 23-7-2004 05:50 PM 说 :
.....
角JAF好像不是PI/6...
角JFA也好像不是PI/3...
我算到tan(角JAF)是0.5
........
m...对。角JAF是 arctan 0.5. = 26.56505118........degree.
给任何正方形,长方形及parallelogram , ABCD/IJKL 都是 5. 这都已被证明了。
只是给任何凸边四角形,要证明 ABCD/IJKL >=5.
这就有点问题了.......... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2004 11:35 PM
|
显示全部楼层
发表于 23-7-2004 11:35 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2004 11:57 AM
|
显示全部楼层
发表于 24-7-2004 11:57 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-7-2004 12:25 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-7-2004 08:52 AM
|
显示全部楼层
发表于 28-7-2004 08:52 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-7-2004 10:50 AM
|
显示全部楼层
发表于 30-7-2004 10:50 AM
|
显示全部楼层
我又想到一题几何题:
我又想到一题几何题:

如上图,点P 与 点Q 分别在AB 与AD 上,使到
三角形 APQ 的周长 是 正方形 ABCD 的周长 的一半。
试证:
(i) 角 PCQ 不变
(ii) 角 PCQ = 45 度 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-7-2004 02:21 PM
|
显示全部楼层
发表于 30-7-2004 02:21 PM
|
显示全部楼层
再来一题几何题:
再来一题几何题:
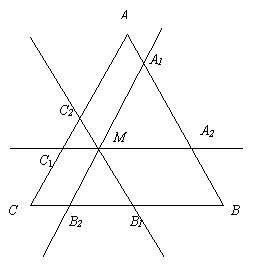
如上图,点 M 是 任意三角形 ABC 里的任意一点。
过 点 M , 画三条分别与 AB,BC 及 CA 平行的线。
S 代表面积。
试证:
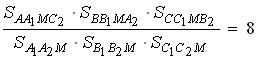 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 1-8-2004 02:29 PM
|
显示全部楼层
pipi 于 28-7-2004 08:52 AM 说 :
以上的问题还没做到。。。  
不过,讲到几何,又讲到凸边四角形,我朋友提出一个有趣的问题(也许独中生在初中时学过了。。。)
任意凸边四角形 ABCD,
取 AB 的中点(设 P )
BC 的中点( ...
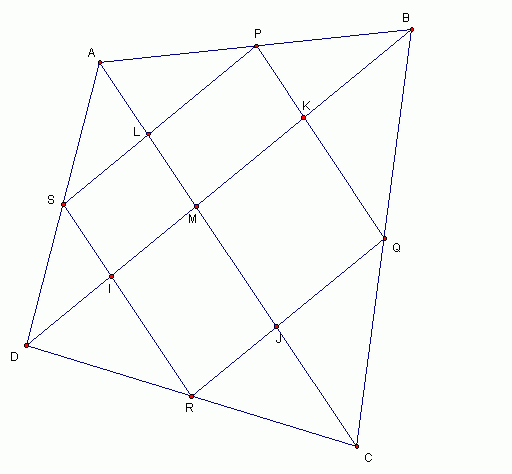
i)
三角形ABC : P,Q 分别是AB,BC 的中心点,所以 PQ//AC ,
以同样的方法,SR//AC。
PQ// AC, SR//AC, 所以 PQ//SR. 再以同样的方法证出 SP//RQ.
PQ//SR, SP//RQ. so, PQRS 是一个平行四方形。
ii)
三角形ABC:
P,Q 分别是AB,BC 的中心点.
所以面积 LPQJ 的高( base) = 面积 PBQ 的高。
LPQJ 的底( height) = 面积 PBQ 的底
so : LPQJ = 2PBQ.
再以同样的方法证出, ISPK = 2ASP,LJRS = 2SRD,IKRQ = 2RQC
so: 2ASP + 2SRD + 2RQC + 2PBQ = 2PQRS
ASP + SRD + RCQ + PBQ = PQRS
ABCD = ASP + SRD + RCQ + PBQ + PQRS
= 2PQRS
[ Last edited by fritlizt on 1-8-2004 at 09:12 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-8-2004 03:58 PM
|
显示全部楼层
发表于 1-8-2004 03:58 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|